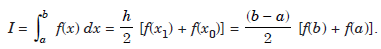Trapezium Rule
The trapezium rule is a way of estimating the area under a curve. It is a rule for estimating the area of an irregular figure, by dividing it into parallel strips of equal width, each strip being a trapezium. It can also be adapted to obtaining an approximate value of a definite integral.This rule is also called the trapezoidal rule.
Let the curve,
y = f(x), a ≤ x ≤ b, be approximated by the line joining the points P(a, f(a)), Q(b, f(b)) on the curve,
Using the Newton’s forward difference formula, the linear polynomial approximation to f(x), interpolating at the points P(a, f(a)), Q(b, f(b)), is given by,
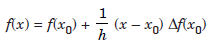......................1.1
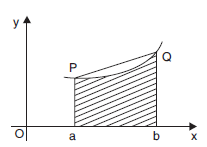
figure : Trapezium rule.
where x0 = a, x1 = b and h = b – a. Substituting in (1.1), we obtain
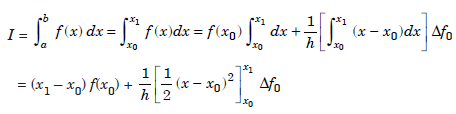
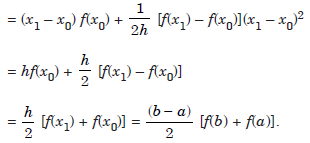
The trapezium rule is given by,
