Per concursum tangentium quarumvis duarum cum se invicem, & concursum tangentis tertiæ cum recta illa, quæ per puncta duo data transit, age rectam infinitam; eaq; adhibita pro radio ordinato primo, transmutetur figura, per Lemma superius, in figuram novam. In hac figura tangentes illæ duæ evadent parallelæ, & tangens tertia fiet parallela rectæ per puncta duo transeunti. Sunto hi, kl tangentes duæ parallelæ, ik tangens tertia, & hl recta huic parallela transiens per puncta illa a, b, per quæ Conica sectio in hac figura nova transire debet, & parallelogrammum hikl complens. Secentur rectæ hi, ik, kl in c, d & e, ita ut sit hc ad latus quadratum rectanguli ahb, ic ad id, & ke ad kd ut est summa rectarum hi & kl ad summam trium linearum quarum prima est recta ik, & alteræ duæ sunt latera quadrata rectangulorum ahb & alb: Et erunt c, d, e puncta contactus. Etenim, ex Conicis, sunt hc quadratum ad rectangulum ahb, & ic quadratum ad id quadratum, & ke quadratum ad kd quadratum, & el quadratum ad alb rectangulum in eadem ratione, & propterea hc ad latus quadratum ipsius ahb, ic ad id, ke ad kd & el ad latus quadratum ipsius alb sunt in dimidiata illa ratione, & composite, in data ratione omnium antecedentium hi & kl ad omnes consequentes, quæ sunt latus quadratum rectanguli ahb & recta ik & latus quadratum rectanguli alb. Habentur igitur ex data illa ratione puncta contactus c, d, e, in figura nova. Per inversas operationes Lemmatis novissimi transferantur hæc puncta in figuram primam & ibi, per casum primum Problematis XIV, describetur Trajectoria. Q. E. F. Cæterum perinde ut puncta a, b jacent vel inter puncta h, l, vel extra, debent puncta c, d, e vel inter puncta h, i, k, l capi, vel extra. Si punctorum a, b alterutrum cadit inter puncta h, l, & alterum extra, Problema impossibile est.
Prop. XXVI. Prob. XVIII.
Trajectoriam describere quæ transibit per punctum datum & rectas quatuor positione datas continget.
Ab intersectione communi duarum quarumlibet tangentium ad intersectionem communem reliquarum duarum agatur recta infinita, & eadem pro radio ordinato primo adhibita, transmutetur figura (per Lem. XXII) in figuram novam, & Tangentes binæ, quæ ad radium ordinatum concurrebant, jam evadent parallelæ. Sunto illæ hi & kl, ik & hl continentes parallelogrammum hikl. Sitq; p punctum in hac nova figura, puncto in figura prima dato respondens. Per figuræ centrum O agatur pq, & existente Oq æquali Op erit q punctum alterum per quod sectio Conica in hac figura nova transire debet. Per Lemmatis XXII operationem inversam transferatur hoc punctum in figuram primam, & ibi habebuntur puncta duo per quæ Trajectoria describenda est. Per eadem vero describi potest Trajectoria illa per Prob. XVII. Q. E. F.
Lemma XXIII.
Si rectæ duæ positione datæ AC, BD ad data puncta A, B terminentur, datamq; habeant rationem ad invicem, & recta CD, qua puncta indeterminata C, D junguntur secetur in ratione data in K: dico quod punctum K locabitur in recta positione data.
Concurrant enim rectæ AC, BD in E, & in BE capiatur BG ad AE ut est BD ad AC, sitq; FD æqualis EG, & erit EC ad GD, hoc est ad EF ut AC ad BD, adeoq; in ratione data, & propterea dabitur specie triangulum EFC. Secetur CF in L in ratione CK ad CD, & dabitur etiam specie triangulum EFL, proindeq; punctum L locabitur in recta EL positione data. Junge LK, & ob datam FD & datam rationem LK ad FD, dabitur LK. Huic æqualis capiatur EH, & erit ELKH parallelogrammum. Locatur igitur punctum K in parallelogrammi latere positione dato HK. Q. E. D.
Lemma XXIV.
Si rectæ tres tangant quamcunq; conisectionem, quarum duæ parallelæ sint ac dentur positione; dico quod sectionis semidiameter hisce duabus parallela, sit media proportionalis inter harum segmenta, punctis contactum & tangenti tertiæ interjecta.
Sunto AF, GB parallelæ duæ Conisectionem ADB tangentes in A & B; EF recta tertia Conisectionem tangens in I, & occurrens prioribus tangentibus in F & G; sitq; CD semidiameter Figuræ tangentibus parallela: Dico quod AF, CD, BG sunt continue proportionales.
Nam si diametri conjugatæ AB, DM tangenti FG occurrant in E & H, seq; mutuo secent in C, & compleatur parallelogrammum IKCL; erit ex natura sectionum Conicarum, ut EC ad CA ita CA ad LC, & ita divisim EC - CA ad CA - CL seu EA ad AL, & composite EA ad EA + AL seu EL ut EC ad EC + CA seu EB; adeoq; (ob similitudinem triangulorum EAF, ELI, ECH, EBG) AF ad LI ut CH ad BG. Est itidem ex natura sectionum Conicarum LI seu CK ad CD ut CD ad CH atq; adeo ex æquo perturbate AF ad CD ut CD ad BG. Q. E. D.
Corol. 1. Hinc si tangentes duæ FG, PQ tangentibus parallelis AF, BG occurrant in F & G, P & Q, seq; mutuo secent in O, erit (ex æquo perturbate) AF ad BQ ut AP ad BG, & divisim ut FP ad GQ, atq; adeo ut FO ad OG.
Corol. 2. Unde etiam rectæ duæ PG, FQ per puncta P & G, F & Q ductæ, concurrent ad rectam ACB per centrum figuræ & puncta contactuum A, B transeuntem.
Lemma XXV.
Si parallelogrammi latera quattuor infinite producta tangant sectionem quamcunq; Conicam & abscindantur ad tangentem quamvis quintam; sumantur autem abscisse terminate ad angulos oppositos parallelogrammi: dico quod abscissa unius lateris ad latus illud, ut pars lateris contermini inter punctum contactus & latus tertium, ad abscissam lateris hujus contermini.
Tangant parallelogrammi MIKL latera quatuor ML, IK, KL, MI sectionem Conicam in A, B, C, D, & secet tangens quinta FQ hæc latera in F, Q, H & E: dico quod sit ME ad MI ut BK ad KQ & KH ad KL ut AM ad MF. Nam per Corollarium Lemmatis superioris, est ME ad EI ut AM seu BK ad BQ, & componendo ME ad MI ut BK ad KQ. Q. E. D. Item KH ad HL ut BK seu AM ad AF, & dividendo KH ad KL ut AM ad MF. Q. E. D.
Corol. 1. Hinc si parallelogrammum IKLM datur, dabitur rectangulum KQ × ME, ut & huic æquale rectangulum KH × MF. Æquantur enim rectangula illa ob similitudinem triangulorum KQH, MFE.
Corol. 2. Et si sexta ducatur tangens eq tangentibus KI, MI occurrens in e & q, rectangulum KQ × ME æquabitur rectangulo Kq × Me, eritq; KQ ad Me ut Kq ad ME, & divisim ut Qq ad Ee.
Corol. 3. Unde etiam si Eq, eQ jungantur & bisecentur, & recta per puncta bisectionum agatur, transibit hæc per centrum Sectionis Conicæ. Nam cum sit Qq ad Ee ut KQ ad Me, transibit eadem recta per medium omnium Eq, eQ, MK; (per Lemma XXIII) & medium rectæ MK est centrum Sectionis.
Prop. XXVII. Prob. XIX.
Trajectoriam describere quæ rectas quinq; positione datas continget.
Dentur positione tangentes ABG, BCF, GCD, FDE, EA. Figuræ quadrilateræ sub quatuor quibusvis contentæ ABFE diagonales AF, BE biseca, & (per Cor. 3. Lem. XXV) recta per puncta bisectionum acta transibit per centrum Trajectoriæ. Rursus figuræ quadrilateræ BGDF, sub alijs quibusvis quatuor tangentibus contentæ, diagonales (ut ita dicam) BD, GF biseca, & recta per puncta bisectionum acta transibit per centrum sectionis. Dabitur ergo centrum in concursu bisecantium. Sit illud O. Tangenti cuivis BC parallelam age KL, ad eam distantiam ut centrum O in medio inter parallelas locetur, & acta KL tanget trajectoriam describendam. Secet hæc tangentes alias quasvis duas CD, FDE in L & K. Per tangentium non parallelarum CL, FK cum parallelis CF, KL concursus C & K, F & L age CK, FL concurrentes in R, & recta OR ducta & producta secabit tangentes parallelas CF, KL in punctis contactuum. Patet hoc per Corol. 2. Lem. XXIV. Eadem methodo invenire licet alia contactuum puncta, & tum demum per Casum 1. Prob. XIV. Trajectoriam describere. Q. E. F.
Schol.
Problemata, ubi dantur Trajectoriarum vel centra vel Asymptoti includuntur in præcedentibus. Nam datis punctis & tangentibus una cum centro, dantur alia totidem puncta aliæq; tangentes a centro ex altera ejus parte æqualiter distantes. Asymptotos autem pro tangente habenda est, & ejus terminus infinite distans (si ita loqui fas sit) pro puncto contactus. Concipe tangentis cujusvis punctum contactus abire in infinitum, & tangens vertetur in Asymptoton, atq; constructiones Problematis XV & Casus primi Problematis XIV vertentur in constructiones Problematum ubi Asymptoti dantur.
Postquam Trajectoria descripta est, invenire licet axes & umbilicos ejus hac methodo. In constructione & Figura Lemmatis XXI, fac ut angulorum mobilium PBN, PCN crura BP, CP quorum concursu Trajectoria describebatur sint sibi invicem parallela, eumq; servantia situm revolvantur circa polos suos B, C in figura illa. Interea vero describant altera angulorum illorum crura CN, BN concursu suo K vel k, circulum IBKGC. Sit circuli hujus centrum O. Ab hoc centro ad Regulam MN, ad quam altera illa crura CN, BN interea concurrebant dum Trajectoria describebatur, demitte normalem OH circulo occurrentem in K & L. Et ubi crura illa altera CK, BK concurrant ad punctum istud K quod Regulæ proprius est, crura prima CP, BP parallela erunt axi majori & perpendicularia minori; & contrarium eveniet si crura eadem concurrunt ad punctum remotius L. Unde si detur Trajectoriæ centrum, dabuntur axes. Hisce autem datis, umbilici sunt in promptu.
Axium vero quadrata sunt ad invicem ut KH ad LH, & inde facile est Trajectoriam specie datam per data quatuor puncta describere. Nam si duo ex punctis datis constituantur poli C, B, tertium dabit angulos mobiles PCK, PBK. Tum ob datam specie Trajectoriam, dabitur ratio OH ad OK, centroq; O & intervallo OH describendo circulum, & per punctum quartum agendo rectam quæ circulum illum tangat, dabitur regula MN cujus ope Trajectoria describatur. Unde etiam vicissim Trapezium specie datum (si casus quidam impossibiles excipiantur) in data quavis sectione Conica inscribi potest.
Sunt & alia Lemmata quorum ope Trajectoriæ specie datæ, datis punctis & tangentibus, describi possunt. Ejus generis est quod, si recta linea per punctum quodvis positione datum ducatur, quæ datam Conisectionem in punctis duobus intersecet, & intersectionum intervallum bisecetur, punctum bisectionis tanget aliam Conisectionem ejusdem speciei cum priore, atq; axes habentem prioris axibus parallelos. Sed propero ad magis utilia.
Lemma XXVI.
Trianguli specie & magnitudine dati tres angulos ad rectas totidem positione datas, quæ non sunt omnes parallelæ, singulos ad singulas ponere.
Dantur positione tres rectæ infinitæ AB, AC, BC,
& oportet triangulum DEF ita locare, ut angulus ejus D
lineam AB, angulus E lineam AC, &
angulus F lineam BC tangat. Super DE, DF
& EF describe tria circulorum segmenta DRE, DGF,
EMF, quæ capiant angulos angulis BAC, ABC,
ACB æquales respective. Describantur autem hæc segmenta ad eas
partes linearum DE, DF, EF ut literæ DRED
eodem ordine cum literis BACB, literæ DGFD eodem cum
literis ABCA, & literæ EMFE eodem cum literis
ACBA in orbem redeant: deinde compleantur hæc  segmenta in circulos. Secent
circuli duo priores se mutuo in G, sintq; centra eorum P
& Q. Junctis GP, PQ, cape Ga ad AB
ut est GP ad PQ, & centro G, intervallo
Ga describe circulum, qui secet circulum primum DGE in
a. Jungatur tum aD secans circulum secundum DFG in
b, tum aE secans circulum tertium GEc in c.
Et compleatur figura ABCdef similis & æqualis figuræ abcDEF. Dico factum.
segmenta in circulos. Secent
circuli duo priores se mutuo in G, sintq; centra eorum P
& Q. Junctis GP, PQ, cape Ga ad AB
ut est GP ad PQ, & centro G, intervallo
Ga describe circulum, qui secet circulum primum DGE in
a. Jungatur tum aD secans circulum secundum DFG in
b, tum aE secans circulum tertium GEc in c.
Et compleatur figura ABCdef similis & æqualis figuræ abcDEF. Dico factum.
Agatur enim Fc ipsi aD occurrens in n. Jungantur aG, bG, PD, QD & producatur PQ ad R. Ex constructione est angulus EaD æqualis angulo CAB, & angulus EcF æqualis angulo ACB, adeoq; triangulum anc triangulo ABC æquiangulum. Ergo angulus anc seu FnD angulo ABC, adeoq; angulo FbD æqualis est, & propterea punctum n incidit in punctum b. Porro angulus GPQ, qui dimidius est anguli ad centrum GPD, æqualis est angulo ad circumferentiam GaD; & angulus GQR, qui dimidius est complementi anguli ad centrum GQD, æqualis est angulo ad circumferentiam GbD, adeoq; eorum complementa PQG, abG æquantur, suntq; ideo triangula GPQ, Gab similia, & Ga est ad ab ut GP ad PQ; id est (ex constructione) ut Ga ad AB. Æquantur itaq; ab & AB, & propterea triangula abc, ABC, quæ modo similia esse probavimus, sunt etiam æqualia. Unde cum tangant insuper trianguli DEF anguli D, E, F trianguli abc latera ab, ac, bc respective, compleri potest figura ABCdef figuræ abcDEF similis & æqualis, atq; eam complendo solvetur Problema. Q. E. F.
Corol. Hinc recta duci potest cujus partes longitudine datæ rectis tribus positione datis interjacebunt. Concipe Triangulum DEF, puncto D ad latus EF accedente, & lateribus DE, DF in directum positis, mutari in lineam rectam, cujus pars data DE, rectis positione datis AB, AC, & pars data DF rectis positione datis AB, BC interponi debet; & applicando constructionem præcedentem ad hunc casum solvetur Problema.
Prop. XXVIII. Prob. XX.
Trajectoriam specie & magnitudine datam describere, cujus partes datæ rectis tribus positione datis interjacebunt.
Describenda sit Trajectoria quæ sit similis & æqualis lineæ curvæ DEF, quæq; a rectis tribus AB, AC, BC positione datis, in partes datis hujus partibus DE & EF similes & æquales secabitur.
Age rectas DE, EF, DF, & trianguli hujus DEF pone angulos D, E, F ad rectas illas positione datas: (per Lem. XXVI) Dein circa triangulum describe Trajectoriam curvæ DEF similem & æqualem. Q. E. F.
Lemma XXVII.
Trapezium specie datum describere cujus anguli ad rectas quatuor positione datas (quæ neq; omnes parallelæ sunt, neq; ad commune punctum convergunt) singuli ad singulas consistent.
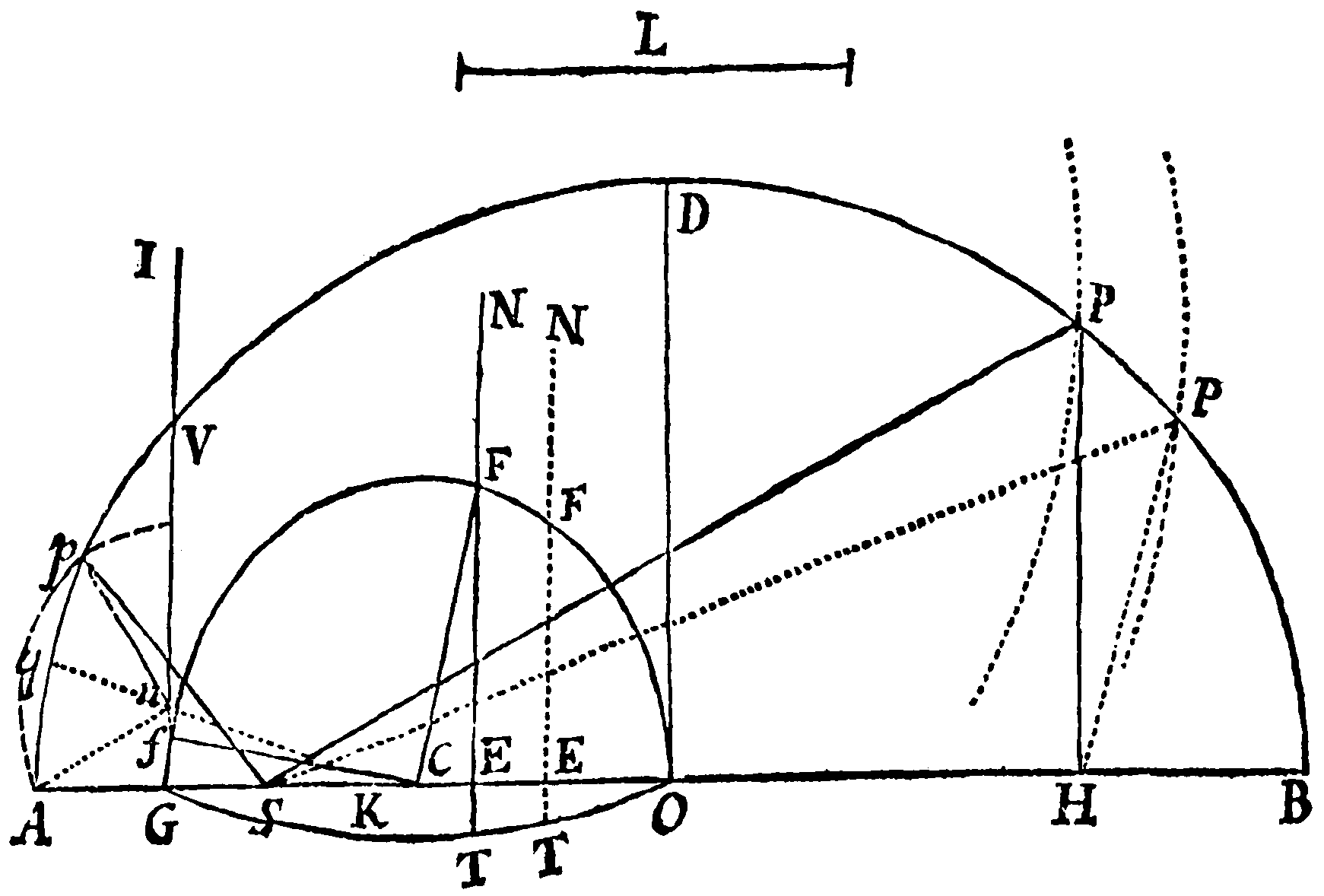
Dentur positione rectæ quatuor ABC, AD, BD, CE, quarum prima secet secundam in A, tertiam in B, & quartam in C: & describendum sit Trapezium fghi quod sit Trapezio FGHI simile, & cujus angulus f, angulo dato F æqualis, tangat rectam ABC cæteriq; anguli g, h, i cæteris angulis datis G, H, I æquales tangant cæteras lineas AD, BD, CE respective. Jungatur FH, & super FG, FH, FI describantur totidem circulorum segmenta FSG, FTH, FVI; quorum primum FSG capiat angulum æqualem angulo BAD, secundum FTH capiat angulum æqualem angulo CBE; ac tertium FVI capiat angulum æqualem angulo ACE. Describi autem debent segmenta ad eas partes linearum FG, FH, FI, ut literarum FSGF idem sit ordo circularis qui literarum BADB, utq; literæ FTHF eodem ordine cum literis CBEC, & literæ FVIF eodem cum literis ACEA in orbem redeant. Compleantur segmenta in circulos, sitq; P centrum circuli primi FSG, & Q centrum secundi FTH. Jungatur & utrinq; producatur PQ, & in ea capiatur QR in ea ratione ad PQ quam habet BC ad AB. Capiatur autem QR ad eas partes puncti Q ut literarum P, Q, R idem sit ordo circularis atq; literarum A, B, C: centroq; R & intervallo RF describatur circulus quartus FNc secans circulum tertium FVI in c. Jungatur Fc secans circulum primum in a & secundum in b. Agantur aG, bH, cI, & figuræ abcFGHI similis constituatur figura ABCfghi: Eritq; Trapezium fghi illud ipsum quod constituere oportuit.
Secent enim circuli duo primi FSG, FTH se mutuo in K. Jungantur PK, QK, RK, aK, bK, cK & producatur QP ad L. Anguli ad circumferentias FaK, FbK, FcK, sunt semisses angulorum FPK, FQK, FRK ad centra, adeoq; angulorum illorum dimidiis LPK, LQK, LRK æquales. Est ergo figura PQRK figuræ abcK æquiangula & similis, & propterea ab est ad bc ut PQ ad QR, id est ut AB ad BC. Angulis insuper FaG, FbH, FcI æquantur fAg, fBh, fCi per constructionem. Ergo figuræ abcFGHI figura similis ABCfghi compleri potest. Quo facto Trapezium fghi constituetur simile Trapezio FGHI & angulis suis f, g, h, i tanget rectas AB, AD, BD, CE. Q. E. F.
Corol. Hinc recta duci potest cujus partes, rectis quatuor positione datis dato ordine interjectæ, datam habebunt proportionem ad invicem. Augeantur anguli FGH, GHI usq; eo, ut rectæ FG, GH, HI in directum jaceant, & in hoc casu construendo Problema, ducetur recta fghi cujus partes fg, gh, hi, rectis quatuor positione datis AB & AD, AD & BD, BD & CE interjectæ, erunt ad invicem ut lineæ FG, GH, HI, eundemq; servabunt ordinem inter se. Idem vero sic fit expeditius.
Producantur AB ad K, & BD ad L, ut sit BK ad AB ut HI ad GH; & DL ad BD ut GI ad FG; & jungatur KL occurrens rectæ CE in i. Producatur iL ad M, ut sit LM ad iL ut GH ad HI, & agatur tum MQ ipsi LB parallela rectæq; AD occurrens in g, tum gi secans AB, BD in f, h. Dico factum.
Secet enim Mg rectam AB in Q, & AD rectam KL in S, & agatur AP, quæ sit ipsi BD parallela & occurrat iL in P, & erunt Mg ad Lh (Mi ad Li, gi ad hi, AK ad BK) & AP ad BL in eadem ratione. Secetur DL in R ut sit DL ad RL in eadem illa ratione, & ob proportionales gS ad gM, AS ad AP & DS ad DL, erit ex æquo ut gS ad Lh ita AS ad BL & DS ad RL; & mixtim, BL - RL ad Lh - BL ut AS - DS ad gS - AS. Id est BR ad Bh ut AD ad Ag, adeoq; ut BD ad gQ. Et vicissim BR ad BD ut Bh ad gQ seu fh ad fg. Sed ex constructione est BR ad BD ut FH ad FG. Ergo fh est ad fg ut FH ad FG. Cum igitur sit etiam ig ad ih ut Mi ad Li, id est, ut IG ad IH, patet lineas FI, fi in g & h, G & H similiter sectas esse. Q. E. F.
In constructione Corollarii hujus postquam ducitur LK secans CE in i, producere licet iE ad V, ut sit EV ad iE ut FH ad HI, & agere Vf parallelam ipsi BD. Eodem recidit si centro i, intervallo IH describatur circulus secans BD in X, producatur iX ad Y, ut sit iY æqualis IF, & agatur Yf ipsi BD parallela.
Prop. XXIX. Prob. XIX.
Trajectoriam specie datam describere, quæ a rectis quatuor positione datis in partes secabitur, ordine, specie & proportione datas.
Describenda sit Trajectoria fghi, quæ similis sit lineæ curvæ FGHI, & cujus partes fg, gh, hi illius partibus FG, GH, HI similes & proportionales, rectis AB & AD, AD & BD, BD & EC positione datis, prima primis, secunda secundis, tertia tertiis interjaceant. Actis rectis FG, GH, HI, FI, describatur Trapezium fghi quod sit Trapezio FGHI simile & cujus anguli f, g, h, i tangant rectas illas positione datas AB, AD, BD, CE singuli singulas dicto ordine. Dein (per Lem. XXVII) circa hoc Trapezium describatur Trajectoria curvæ lineæ FGHI consimilis.
Scholium.
Construi etiam potest hoc Problema ut sequitur. Junctis FG, GH, HI, FI produc GF ad V, jungeq; FH, IG, & angulis FGH, VFH fac angulos CAK, DAL æquales. Concurrant AK, AL cum recta BD in K & L, & inde aguntur KM, LN, quarum KM constituat angulum AKM æqualem angulo GHI, sitq; ad AK ut est HI ad GH; & LN constituat angulum ALN æqualem angulo FHI, sitq; ad AL ut HI ad FH. Ducantur autem AK, KM, AL, LN ad eas partes linearum AD, AK, AL, ut literæ CAKMC, ALK, DALND eodem ordine cum literis FGHIF in orbem redeant, & acta MN occurrat rectæ CE in i. Fac angulum iEP æqualem angulo IGF, sitq; PE ad Ei ut FG ad GI; & per P agatur QPf, quæ cum recta AED contineat angulum PQE æqualem angulo FIG, rectæq; AB occurrat in f, & jungatur fi. Agantur autem PE & PQ ad eas partes linearum CE, PE, ut literarum PEiP & PEQP idem sit ordo circularis qui literarum FGHIF, & si super linea fi eodem quoq; literarum ordine constituatur Trapezium fghi Trapezio FGHI simile, & circumscribatur Trajectoria specie data, solvetur Problema.
Hactenus de orbibus inveniendis. Superest ut motus corporum orbibus inventis determinemus.
SECT. VI.
De inventione motuum in Orbibus datis.
Prop. XXX. Prob. XXII.
Corporis in data Trajectoria Parabolica moventis, invenire locum ad tempus assignatum.
Sit S umbilicus & A vertex principalis Parabolæ, sitq; 4AS × M area Parabolica APS, quæ radio SP, vel post excessum corporis de vertice descripta fuit, vel ante appulsum ejus ad verticem describenda est. Innotescit area illa ex tempore ipsi proportionali. Biseca AS in G, erigeq; perpendiculum GH æquale 3M, & circulus centro H, intervallo HS descriptus secabit Parabolam in loco quæsito P. Nam demissa ad axem perpendiculari PO, est HGq. + GSq. (= HSq. = HPq. = GOq. + PO - HGq.) = GOq. + HGq. - 2HG × PO + POq. Et deleto utrinq; HGq. fiet GSq. = GOq. - 2HG × PO + POq. seu 2HG × PO (= GOq. + POq. - GSq. = AOq. - 2GAO + POq.) = AOq. + ¾POq. Pro AOq. scribe AO × POq. ÷ 4AS, & applicatis terminis omnibus ad 3PO, ductisq; in 2AS, fiet 4/3GH × AS (= 1/6AO × PO + ½AS × PO = {AO + 3AS} ÷ 6 × PO = {4AO - 3SO} ÷ 6 × PO = areæ APO - SPO) = areæ APS. Sed GH erat 3M, & inde 4/3HG × AS est 4AS × M. Ergo area APS æqualis est 4AS × M. Q. E. D.
Corol. 1. Hinc GH est ad AS, ut tempus quo corpus descripsit arcum AP ad tempus quo corpus descripsit arcum inter verticem A & perpendiculum ad axem ab umbilico S erectum.
Corol. 2. Et circulo ASP per corpus movens perpetuo transeunte, velocitas puncti H est ad velocitatem quam corpus habuit in vertice A, ut 3 ad 8; adeoq; in ea etiam ratione est linea GH ad lineam rectam quam corpus tempore motus sui ab A ad P, ea cum velocitate quam habuit in vertice A, describere posset.
Corol. 3. Hinc etiam viceversa inveniri potest tempus quo corpus descripsit arcum quemvis assignatum AP. Junge AP & ad medium ejus punctum erige perpendiculum rectæ GH occurrens in H.
Lemma XXVIII.
Nulla extat figura Ovalis cujus area, rectis pro lubitu abscissa, possit per æquationes numero terminorum ac dimensionum finitas generaliter inveniri.
Intra Ovalem detur punctum quodvis, circa quod ceu polum revolvatur perpetuo linea recta, & interea in recta illa exeat punctum mobile de polo, pergatq; semper ea cum velocitate, quæ sit ut rectæ illius intra Ovalem longitudo. Hoc motu punctum illud describet Spiralem gyris infinitis. Jam si area Oualis per finitam æquationem inveniri potest, invenietur etiam per eandem æquationem distantia puncti a polo; quæ huic areæ proportionalis est, adeoq; omnia Spiralis puncta per æquationem finitam inveniri possunt: & propterea rectæ cujusvis positione datæ intersectio cum spirali inveniri etiam potest per æquationem finitam. Atqui recta omnis infinite producta spiralem secat in punctis numero infinitis, & æquatio, qua intersectio aliqua duarum linearum invenitur, exhibet earum intersectiones omnes radicibus totidem, adeoq; ascendit ad tot dimensiones quot sunt intersectiones. Quoniam circuli duo se mutuo secant in punctis duobus, intersectio una non invenitur nisi per æquationem duarum dimensionum, qua intersectio altera etiam inveniatur. Quoniam duarum sectionum Conicarum quatuor esse possunt intersectiones, non potest aliqua earum generaliter inveniri nisi per æquationem quatuor dimensionum, qua omnes simul inveniantur. Nam si intersectiones illæ seorsim quærantur, quoniam eadem est omnium lex & conditio, idem erit calculus in casu unoquoq; & propterea eadem semper conclusio, quæ igitur debet omnes intersectiones simul complecti & indifferenter exhibere. Unde etiam intersectiones Sectionum Conicarum & curvarum tertiæ potestatis, eo quod sex esse possunt, simul prodeunt per æquationes sex dimensionum, & intersectiones duarum curvarum tertiæ potestatis, quia novem esse possunt, simul prodeunt per æquationes dimensionum novem. Id nisi necessario fieret, reducere liceret Problemata omnia Solida ad Plana, & plusquam solida ad solida. Eadem de causa intersectiones binæ rectarum & sectionum Conicarum prodeunt semper per æquationes duarum dimensionum; ternæ rectarum & curvarum tertiæ potestatis per æquationes trium, quaternæ rectarum & curvarum quartæ potestatis per æquationes dimensionum quatuor, & sic in infinitum. Ergo intersectiones numero infinitæ rectarum, propterea quod omnium eadem est lex & idem calculus, requirunt æquationes numero dimensionum & radicum infinitas, quibus omnes possunt simul exhiberi. Si a polo in rectam illam secantem demittatur perpendiculum, & perpendiculum una cum secante revolvatur circa polum, intersectiones spiralis transibunt in se mutuo, quæq; prima erat seu proxima, post unam revolutionem secunda erit, post duas tertia, & sic deinceps: nec interea mutabitur æquatio nisi pro mutata magnitudine quantitatum per quas positio secantis determinatur. Unde cum quantitates illæ post singulas revolutiones redeunt ad magnitudines primas, æquatio redibit ad formam primam, adeoq; una eademq; exhibebit intersectiones omnes, & propterea radices habebit numero infinitas, quibus omnes exhiberi possunt. Nequit ergo intersectio rectæ & spiralis per æquationem finitam generaliter inveniri, & idcirco nulla extat Ovalis cujus area, rectis imperatis abscissa, possit per talem æquationem generaliter exhiberi.
Eodem argumento, si intervallum poli & puncti, quo spiralis describitur, capiatur Ovalis perimetro abscissæ proportionale, probari potest quod longitudo perimetri nequit per finitam æquationem generaliter exhiberi.
Corollarium.
Hinc area Ellipseos, quæ radio ab umbilico ad corpus mobile ducto describitur, non prodit ex dato tempore, per æquationem finitam; & propterea per descriptionem Curuarum Geometrice rationalium determinari nequit. Curvas Geometrice rationales appello quarum puncta omnia per longitudines æquationibus definitas, id est, per longitudinum rationes complicatas, determinari possunt; cæterasq; (ut Spirales, Quadratrices, Trochoides) Geometrice irrationales. Nam longitudines quæ sunt vel non sunt ut numerus ad numerum (quemadmodum in decimo Elementorum) sunt Arithmetice rationales vel irrationales. Aream igitur Ellipseos tempori proportionalem abscindo per Curvam Geometrice irrationalem ut sequitur.
Prop. XXXI. Prob. XXIII.
Corporis in data Trajectoria Elliptica moventis invenire locum ad tempus assignatum.
Ellipseos APB sit A vertex principalis, S umbilicus, O centrum, sitq; P corporis locus inveniendus. Produc OA ad G ut sit OG ad OA ut OA ad OS. Erige perpendiculum GH, centroq; O & intervallo OG describe circulum EFG, & super regula GH, ceu fundo, progrediatur rota GEF revolvendo circa axem suum, & interea puncto suo A describendo Trochoidem ALI. Quo facto, cape GK in ratione ad rotæ perimetrum GEFG, ut est tempus quo corpus progrediendo ab A descripsit arcum AP, ad tempus revolutionis unius in Ellipsi. Erigatur perpendiculum KL occurrens Trochoidi in L, & acta LP ipsi KG parallela occurret Ellipsi in corporis loco quæsito P.
Nam centro O intervallo OA describatur semicirculus AQB, & arcui AQ occurrat LP producta in Q, junganturq; SQ, OQ. Arcui EFG occurrat OQ in F, & in eandem OQ demittatur perpendiculum SR. Area APS est ut area AQS, id est, ut differentia inter sectorem OQA & triangulum OQS, sive ut differentia rectangulorum ½Q × AQ & ½OQ × SR, hoc est, ob datam ½OQ, ut differentia inter arcum AQ & rectam SR, adeoq; (ob æqualitatem rationum SR ad sinum arcus AQ, OS ad OA, OA ad OG, AQ ad GF, & divisim AQ - SR ad GF - sin. arc. AQ) ut GK differentia inter arcum GF & sinum arcus AQ. Q. E. D.
Scholium.
Cæterum ob difficultatem describendi hanc curvam præstat constructiones vero proximas in praxi Mechanica adhibere. Ellipseos cujusvis APB sit AB axis major, O centrum, S umbilicus, OD semiaxis minor, & AK dimidium lateris recti. Secetur AS in G, ut sit AG ad AS ut BO ad BS; & quæratur longitudo L, quæ sit ad ½GK ut est AO quad. ad rectangulum AS × OD. Bisecetur OG in C, centroq; C & intervallo CG describatur semicirculus GFO. Deniq; capiatur angulus GCF in ea ratione ad angulos quatuor rectos, quam habet tempus datum, quo corpus descripsit arcum quæsitum AP, ad tempus periodicum seu revolutionis unius in Ellipsi: Ad AO demittatur normalis FE, & producatur eadem versus F ad usq; N, ut sit EN ad longitudinem L, ut anguli illius sinus EF ad radium CF; centroq; N & intervallo AN descriptus circulus secabit Ellipsin in corporis loco quæsito P quam proxime.
Nam completo dimidio temporis periodici, corpus P semper reperietur in Apside summa B, & completo altero temporis dimidio, redibit ad Apsidem imam, ut oportet. Ubi vero proxime abest ab Apsidibus, ratio prima nascentium sectorum ASP, GCF, & ratio ultima evanescentium BSP & OCF, eadem est rationi Ellipseos totius ad circulum totum. Nam punctis P, F & N incidentibus in loca p, f & n axi AB quam proximis; ob æquales An, pn, recta nq, quæ ad arcum Ap perpendicularis est, adeoq; concurrit cum axe in puncto K, bisecat arcum Ap. Proinde est ½Ap ad Gn ut AK ad GK, & Ap ad Gn ut 2AK ad GK. Est & Gn ad Gf ut EN ad EF, seu L ad CF, id est, ut {GK × AOq.} ÷ {2AS × OD} ad CF, seu GK × AOq. ad 2AS × OD × CF, & ex æquo Ap ad Gf ut 2AK ad GK + GK × AOq. ad 2AS × OD × CF, id est, ut AK × AOq. ad AS × OD × CF, hoc est, ob æqualia AK × AO × ODq. ut AO × OD ad AS × CF. Proinde Ap × ½AS est ad Gf × ½GC ut AO × OD × AS ad AS × CF × GC, seu AO × OD ad CGq. id est, sector nascens ASp ad sectorem nascentem GCf ut AO × OD ad CGq. & propterea ut area Ellipseos totius ad aream circuli totius. Q. E. D. Argumento prolixiore probari potest analogia ultima in Sectoribus evanescentibus BSP, OCF: ideoq; locus puncti P prope Apsides satis accurate inventus est. In quadraturis error quasi quingentesimæ partis areæ Ellipseos totius vel paulo major obvenire solet: qui tamen propemodum evanescet per ulteriorem Constructionem sequentem.
Per puncta G, O, duc arcum circularem GTO justæ magnitudinis; dein produc EF hinc inde ad T & N ut sit EN ad FT ut ½L ad CF; centroq; N & intervallo AN describe circulum qui secet Ellipsin in P, ut supra. Arcus autem GTO determinabitur quærendo ejus punctum aliquod T; quod constructionem in illo casu accuratam reddet.
Si Ellipseos latus transversum multo majus sit quam latus rectum, & motus corporis prope verticem Ellipseos desideretur, (qui casus in Theoria Cometarum incidit,) educere licet e puncto G rectam GI axi AB perpendicularem, & in ea ratione ad GK quam habet area AVPS ad rectangulum AK × AS; dein centro I & intervallo AI circulum describere. Hic enim secabit Ellipsim in corporis loco quæsito P quamproxime. Et eadem constructione (mutatis mutandis) conficitur Problema in Hyperbola. Hæ autem constructiones demonstrantur ut supra, & si Figura (vertice ulteriore B in infinitum abeunte) vertatur in Parabolam, migrant in accuratam illam constructionem Problematis XXII.