Corol. 4. Et universaliter, si corporis altitudo maxima CV nominetur T, & radius curvaturæ quam Orbis VPK habet in V, id est radius circuli æqualiter curvi, nominetur R, & vis centripeta qua corpus in Trajectoria quacunq; immobili VPK revolvi potest, in loco V dicatur {Fq. ÷ Tq.} V, atq; aliis in locis P indefinite dicatur X, altitudine CP nominata A, & capiatur G ad F in data ratione anguli VCp ad angulum VCP: erit vis centripeta qua corpus idem eosdem motus in eadem Trajectoria vpk circulariter mota temporibus iisdem peragere potest, ut summa virium X + {VRGq. - VRFq.} ÷ A cub.
Corol. 5. Dato igitur motu corporis in Orbe quocunq; immobili, augeri vel minui potest ejus motus angularis circa centrum virium in ratione data, & inde inveniri novi orbes immobiles in quibus corpora novis viribus centripetis gyrentur.
Corol. 6. Igitur si ad rectam CV positione datam erigatur perpendiculum VP longitudinis indeterminatæ, jungaturq; PC, & ipsi æqualis agatur Cp, constituens angulum VCp, qui sit ad angulum VCP in data ratione; vis qua corpus gyrari potest in Curva illa Vpk quam punctum p perpetuo tangit, erit reciproce ut cubus altitudinis Cp. Nam corpus P, per vim inertiæ, nulla alia vi urgente, uniformiter progredi potest in recta VP. Addatur vis in centrum C, cubo altitudinis CP vel Cp reciproce proportionalis, & (per jam demonstrata) detorquebitur motus ille rectilineus in lineam curvam Vpk. Est autem hæc Curva Vpk eadem cum Curva illa VPQ in Corol. 3. Prop. XLI inventa, in qua ibi diximus corpora hujusmodi viribus attracta oblique ascendere.
Prop. XLV. Prob. XXXI.
Orbium qui sunt Circulis maxime finitimi requiruntur motus Apsidum.
Problema solvitur Arithmetice faciendo ut orbis, quem corpus in Ellipsi mobili, ut in Propositionis superioris Corol. 2. vel 3. revolvens, describit in plano immobili, accedat ad formam orbis cujus Apsides requiruntur, & quærendo Apsides orbis quem corpus illud in plano immobili describit. Orbes autem eandem acquirent formam, si vires centripetæ quibus describuntur, inter se collatæ, in æqualibus altitudinibus reddantur proportionales. Sit punctum V Apsis summa, & scribantur T pro altitudine maxima CV, A pro altitudine quavis alia CP vel Cp, & X pro altitudinum differentia CV - CP; & vis qua corpus in Ellipsi circa umbilicum ejus C (ut in Corollario 2.) revolvente movetur, quæq; in Corollario 2. erat ut Fq. ÷ Aq. + {RGq. - RFq.} ÷ A cub. id est ut {Fq. A + RGq. - RFq.} ÷ A cub., substituendo T - X pro A, erit ut {RGq. - RFq. + TFq. - Fq.X} ÷ A cub. Reducenda similiter est vis alia quævis centripeta ad fractionem cujus denominator sit A cub. & numeratores, facta homologorum terminorum collatione, statuendi sunt analogi. Res Exemplis parebit.
Exempl. 1. Ponamus vim centripetam uniformem esse, adeoq; ut A cub. ÷ A cub., sive (scribendo T - X pro A in Numeratore) ut {T cub. - 3Tq.X + 3TXq. - X cub.} ÷ A cub.; & collatis Numeratorum terminis correspondentibus, nimirum datis cum datis & non datis cum non datis, fiet RGq. - RFq. + TFq. ad T cub. ut -Fq.X ad -3Tq.X + 3TXq. - X cub. sive ut -Fq. ad -3Tq. + 3TX - Xq. Jam cum Orbis ponatur circulo quam maxime finitimus, coeat orbis cum circulo; & ob factas R, T æquales, atq; X in infinitum diminutam, rationes ultimæ erunt RGq. ad T cub. ut -Fq. ad -3Tq. seu Gq. ad Tq. ut Fq. ad 3Tq. & vicissim G quadrat. ad F quadrat. ut T quad. ad 3T quad. id est, ut 1 ad 3; adeoq; G ad F, hoc est angulus VCp ad angulum VCP ut 1 ad √3. Ergo cum corpus in Ellipsi immobili, ab Apside summa ad Apsidem imam descendendo conficiat angulum VCP (ut ita dicam) graduum 180; corpus aliud in Ellipsi mobili, atq; adeo in orbe immobili de quo agimus, ab Abside summa ad Apsidem imam descendendo conficiet angulum VCp graduum 180 ÷ √3: id adeo ob similitudinem orbis hujus, quem corpus agente uniformi vi centripeta describit, & orbis illius quem corpus in Ellipsi revolvente gyros peragens describit in plano quiescente. Per superiorem terminorum collationem similes redduntur hi orbes, non universaliter, sed tunc cum ad formam circularem quam maxime appropinquant. Corpus igitur uniformi cum vi centripeta in orbe propemodum circulari revolvens, inter Apsidem summam & Apsidem imam conficiet semper angulum 180 ÷ √3 graduum, seu 103 gr. 55 m. ad centrum; perveniens ab Apside summa ad Apsidem imam, ubi semel confecit hunc angulum, & inde ad Apsidem summam rediens, ubi iterum confecit eundem angulum, & sic deinceps in infinitum.
Exempl. 2. Ponamus vim centripetam esse ut altitudinis A dignitas quælibet An - 3 seu An ÷ A3: ubi n - 3 & n significant dignitatum indices quoscunq; integros vel fractos, rationales vel irrationales, affirmativos vel negativos. Numerator ille An seu T - X n in seriem indeterminatam per Methodum nostram Serierum convergentium reducta, evadit Tn - nXTn - 1 + {nn - n}÷2 Xq.Tn - 2 &c. Et collatis hujus terminis cum terminis Numeratoris alterius RGq. - RFq. + TFq. - Fq.X, fit RGq. - RFq. + TFq. ad Tn ut -Fq. ad -nTn - 1 + {nn - n}÷2 XTn - 2 &c. Et sumendo rationes ultimas ubi orbes ad formam circularem accedunt, fit RGq. ad Tn ut -Fq. ad -nTn - 1, seu Gq. ad Tn - 1 ut Fq. ad nTn - 1, & vicissim Gq. ad Fq. ut Tn - 1 ad nTn - 1 id est ut 1 ad n; adeoq; G ad F, id est angulus VCp ad angulum VCP, ut 1 ad √n. Quare cum angulus VCP, in descensu corporis ab Apside summa ad Apsidem imam in Ellipsi confectus, sit graduum 180, conficietur angulus VCp, in descensu corporis ab Apside summa ad Apsidem imam in Orbe propemodum circulari, quem corpus quodvis vi centripeta dignitati An - 3 proportionali describit, æqualis angulo graduum 180 ÷ √n; & hoc angulo repetito corpus redibit ab Apside ima ad Apsidem summam, & sic deinceps in infinitum. Ut si vis centripeta sit ut distantia corporis a centro, id est ut A seu A4 ÷ A3, erit n æqualis 4 & √4 æqualis 2; adeoq; angulus inter Apsidem summam & Apsidem imam æqualis 180 ÷ 2 gr. seu 90 gr. Completa igitur quarta parte revolutionis unius corpus perveniet ad Apsidem imam, & completa alia quarta parte ad Apsidem summam, & sic deinceps per vices in infinitum. Id quod etiam ex Propositione X. manifestum est. Nam corpus urgente hac vi centripeta revolvetur in Ellipsi immobili, cujus centrum est in centro virium. Quod si vis centripeta sit reciproce ut distantia, id est directe ut 1 ÷ A seu A2 ÷ A3, erit n = 2, adeoq; inter Apsidem summam & imam angulus erit graduum 180 ÷ √2 seu 127 gr. 17 min. & propterea corpus tali vi revolvens, perpetua anguli hujus repetitione, vicibus alternis ab Apside summa ad imam & ab ima ad summam perveniet in æternum. Porro si vis centripeta sit reciproce ut Latus quadrato-quadratum undecimæ dignitatis Altitudinis, id est reciproce ut A11/4, adeoq; directe ut 1 ÷ A11/4 seu ut A¼ ÷ A3 erit n æqualis ¼, & 180 ÷ √n gr. æqualis 360 gr. & propterea corpus de Apside summa discedens & subinde perpetuo descendens, perveniet ad Apsidem imam ubi complevit revolutionem integram, dein perpetuo ascensu complendo aliam revolutionem integram, redibit ad Apsidem summam: & sic per vices in æternum.
Exempl. 3. Assumentes m & n pro quibusvis indicibus dignitatum Altitudinis, & b, c pro numeris quibusvis datis, ponamus vim centripetam esse ut {bAm + cAn} ÷ A cub. id est ut {b in T - Xm + c in T - Xn} ÷ A cub. seu (per eandem Methodum nostram Serierum convergentium) ut
| bTm - mbXTm - 1 + {mm - m}÷2 bX2Tm - 2 + cTn - ncXTn - 1 + {nn - n}÷2 cX2Tn - 2 &c. |
| A cub. |
& collatis numeratorum terminis, fiet RGq. - RFq. + TFq. ad bTm + cTn, ut -Fq. ad -mbTm - 1 - ncTn - 1 + {mm - m}÷2 XTm - 2 + {nn - n}÷2 XTn - 2 &c. Et sumendo rationes ultimas quæ prodeunt ubi orbes ad formam circularem accedunt, fit Gq. ad bTm - 1 + cTn - 1, ut Fq. ad mbTm - 1 + ncTn - 1, & vicissim Gq. ad Fq. ut bTm - 1 + cTn - 1 ad mbTm - 1 + ncTn - 1. Quæ proportio, exponendo altitudinem maximam CV seu T Arithmetice per unitatem, fit Gq. ad Fq. ut b + c ad mb + nc, adeoq; ut 1 ad {mb + nc} ÷ {b + c}. Unde est G ad F, id est angulus VCp ad angulum VCP, ut 1 ad √{{mb + nc} ÷ {b + c}}. Et propterea cum angulus VCP inter Apsidem summam & Apsidem imam in Ellipsi immobili sit 180 gr. erit angulus VCp inter easdem Apsides, in Orbe quem corpus vi centripeta quantitati {bAm + cAn} ÷ A cub. proportionali describit, æqualis angulo graduum 180 √{{b + c} ÷ {mb + nc}}. Et eodem argumento si vis centripeta sit ut {bAm - cAn} ÷ A cub., angulus inter Apsides invenietur 180 √{{b - c} ÷ {mb - nc}} graduum. Nec secus resolvetur Problema in casibus difficilioribus. Quantitas cui vis centripeta proportionalis est, resolvi semper debet in series convergentes denominatorem habentes A cub. Dein pars data Numeratoris hujus RGq. - RFq. + TFq. - Fq.X ad partem non datam in eadem ratione ponendæ sunt: Et quantitates superfluas delendo, scribendoq; unitatem pro T, obtinebitur proportio G ad F.
Corol. 1. Hinc si vis centripeta sit ut aliqua altitudinis dignitas, inveniri potest dignitas illa ex motu Apsidum; & contra. Nimirum si motus totus angularis, quo corpus redit ad Apsidem eandem, sit ad motum angularem revolutionis unius, seu graduum 360, ut numerus aliquis m ad numerum alium n, & altitudo nominetur A: erit vis ut altitudinis dignitas illa Ann/mm - 3, cujus Index est nn/mm - 3. Id quod per Exempla secunda manifestum est. Unde liquet vim illam in majore quam triplicata altitudinis ratione decrescere non posse: Corpus tali vi revolvens deq; Apside discedens, si cæperit descendere, nunquam perveniet ad Apsidem imam seu altitudinem minimam, sed descendet usq; ad centrum, describens curvam illam lineam de qua egimus in Corol. 3. Prop. XLI. Sin cæperit illud de Apside discedens vel minimum ascendere, ascendet in infinitum, neq; unquam perveniet ad Apsidem summam. Describet enim curvam illam lineam de qua actum est in eodem Corol. & in Corol. 6. Prop. XLIV. Sic & ubi vis in recessu a centro decrescit in majori quam triplicata ratione altitudinis, corpus de Apside discedens, perinde ut cæperit descendere vel ascendere, vel descendet ad centrum usq; vel ascendet in infinitum. At si vis in recessu a centro vel decrescat in minori quam triplicata ratione altitudinis, vel crescat in altitudinis ratione quacunq; Corpus nunquam descendet ad centrum usq; sed ad Apsidem imam aliquando perveniet: & contra, si corpus de Apside ad Apsidem alternis vicibus descendens & ascendens nunquam appellat ad centrum, Vis in recessu a centro aut augebitur, aut in minore quam triplicata altitudinis ratione decrescet: & quo citius corpus de Apside ad Apsidem redierit, eo longius ratio virium recedet a ratione illa triplicata. Ut si corpus revolutionibus 8 vel 4 vel 2 vel 11/2 de Apside summa ad Apsidem summam alterno descensu & ascensu redierit, hoc est, si fuerit m ad n ut 8 vel 4 vel 2 vel 11/2 ad 1, adeoq; nn/mm - 3 ualeat 1/64 - 3 vel 1/16 - 3 vel 1/4 - 3 vel 4/9 - 3, erit vis ut A1/64 - 3 vel A1/16 - 3 vel A1/4 - 3 vel A4/9 - 3, id est reciproce ut A3 - 1/64 vel A3 - 1/16 vel A3 - 1/4 vel A3 - 4/9. Si corpus singulis revolutionibus redierit ad Apsidem eandem immotam, erit m ad n ut 1 ad 1, adeoq; Ann/mm - 3 æqualis A-2 seu 1 ÷ A2, & propterea decrementum virium in ratione duplicata altitudinis, ut in præcedentibus demonstratum est. Si corpus partibus revolutionis unius vel tribus quartis, vel duabus tertiis, vel una tertia, vel una quarta, ad Apsidem eandem redierit, erit m ad n ut 3/4 vel 2/3 vel 1/3 vel 1/4 ad 1, adeoq; Ann/mm - 3 æqualis A16/9 - 3 vel A9/4 - 3 vel A9 - 3 vel A16 - 3 & propterea Vis aut reciproce ut A11/9 vel A3/4, aut directe ut A6 vel A13. Deniq; si Corpus pergendo ab Apside summa ad Apsidem summam confecerit revolutionem integram, & præterea gradus tres, adeoq; Apsis illa singulis corporis revolutionibus confecerit in Consequentia gradus tres, erit m ad n ut 363gr. ad 360gr. adeoq; Ann/mm - 3 erit æquale A-265707÷131769, & propterea Vis centripeta reciproce ut A265707÷131769 seu A24/243. Decrescit igitur Vis centripeta in ratione paulo majore quam duplicata, sed quæ vicibus 603/4 propius ad duplicatam quam ad triplicatam accedit.
Corol. 2. Hinc etiam si corpus, vi centripeta quæ sit reciproce ut quadratum altitudinis, revolvatur in Ellipsi umbilicum habente in centro virium, & huic vi centripetæ addatur vel auferatur vis alia quævis extranea; cognosci potest (per Exempla tertia) motus Apsidum qui ex vi illa extranea orietur: & contra. Ut si vis qua corpus revolvitur in Ellipsi sit ut 1 ÷ A2, & vis extranea ablata ut cA, adeoq; vis reliqua ut {A - cA4} ÷ A3; erit (in Exemplis tertiis) A æqualis 1 & n æqualis 4, adeoq; angulus revolutionis inter Apsides æqualis angulo graduum 180√{{1 - c} ÷ {1 - 4c}}. Ponatur vim illam extraneam esse 357,45 vicibus minorem quam vis altera qua corpus revolvitur in Ellipsi, id est c esse 100 ÷ 35745, & 180√{{1 - c} ÷ {1 - 4c}} evadet 180√{35645 ÷ 35345} seu 180,7602, id est 180gr. 45m. 37s. Igitur corpus de Apside summa discedens, motu angulari 180gr. 45m. 37s. perveniet ad Apsidem imam, & hoc motu duplicato ad Apsidem summam redibit: adeoq; Apsis summa singulis revolutionibus progrediendo conficiet 1gr. 31m. 14s.
Hactenus de motu corporum in orbibus quorum plana per centrum virium transeunt. Superest ut motus etiam determinemus in planis excentricis. Nam Scriptores qui motum gravium tractant, considerare solent ascensus & descensus ponderum, tam obliquos in planis quibuscunq; datis, quam perpendiculares: & pari jure motus corporum viribus quibuscunq; centra petentium, & planis excentricis innitentium hic considerandus venit. Plana autem supponimus esse politissima & absolute lubrica ne corpora retardent. Quinimo in his demonstrationibus, vice planorum quibus corpora incumbunt quasq; tangunt incumbendo, usurpamus plana his parallela, in quibus centra corporum moventur & orbitas movendo describunt. Et eadem lege motus corporum in superficiebus curvis peractos subinde determinamus.
SECT. X.
De Motu Corporum in Superficiebus datis, deq; Funipendulorum Motu reciproco.
Prop. XLVI. Prob. XXXII.
Posita cujuscunq; generis vi centripeta, datoq; tum virium centro tum plano quocunq; in quo corpus revolvitur, & concessis Figurarum curvilinearum quadraturis: requiritur motus corporis de loco dato data cum velocitate secundum Rectam in Plano illo datam egressi.
Sit S centrum virium, SC distantia minima centri hujus a plano dato, P corpus de loco P secundum rectam PZ egrediens, Q corpus idem in Trajectoria sua revolvens, & PQR Trajectoria illa in plano dato descripta, quam invenire oportet. Jungantur CQ, QS, & si in QS capiatur SV proportionalis vi centripetæ qua corpus trahitur versus centrum S, & agatur VT quæ sit parallela CQ & occurrat SC in T: Vis SV resolvetur (per Legum Corol. 2.) in vires ST, TV; quarum ST trahendo corpus secundum lineam plano perpendicularem, nil mutat motum ejus in hoc plano. Vis autem altera TV, agendo secundum positionem plani, trahit corpus directe versus punctum C in plano datum, adeoq; facit illud in hoc plano perinde moveri ac si vis ST tolleretur, & corpus vi sola TV revolveretur circa centrum C in spatio libero. Data autem vi centripeta TV qua corpus Q in spatio libero circa centrum datum C revolvitur, datur per Prop. XLII. tum Trajectoria PQR quam corpus describit, tum locus Q in quo corpus ad datum quodvis tempus versabitur, tum deniq; velocitas corporis in loco illo Q; & contra. Q. E. I.
Prop. XLVII. Theor. XV.
Posito quod vis centripeta proportionalis sit distantiæ corporis a centro; corpora omnia in planis quibuscunq; revolventia describent Ellipses, & revolutiones temporibus æqualibus peragent; quæq; moventur in lineis rectis ultro citroq; discurrendo, singulas eundi & redeundi periodos iisdem temporibus absolvent.
Nam stantibus quæ in superiore Propositione; vis SV qua corpus Q in plano quovis PQR revolvens trahitur versus centrum S est ut distantia SQ; atq; adeo ob proportionales SV & SQ, TV & CQ, vis TV qua corpus trahitur versus punctum C in Orbis plano datum, est ut distantia CQ. Vires igitur, quibus corpora in plano PQR versantia trahuntur versus punctum C, sunt pro ratione distantiarum æquales viribus quibus corpora unaquaq; trahuntur versus centrum S; & propterea corpora movebuntur iisdem temporibus in iisdem figuris in plano quovis PQR circa punctum C, atq; in spatiis liberis circa centrum S, adeoq; (per Corol. 2. Prop. X. & Corol. 2. Prop. XXXVIII.) temporibus semper æqualibus, vel describent Ellipses in plano illo circa centrum C, vel periodos movendi ultro citroq; in lineis rectis per centrum C in plano illo ductis, complebunt. Q. E. D.
Scholium.
His affines sunt ascensus ac descensus corporum in superficiebus curvis. Concipe lineas curvas in plano describi, dein circa axes quosvis datos per centrum virium transeuntes revolvi, & ea revolutione superficies curvas describere; tum corpora ita moveri ut eorum centra in his superficiebus perpetuo reperiantur. Si corpora illa oblique ascendendo & descendendo currant ultro citroq; peragentur eorum motus in planis per axem transeuntibus, atq; adeo in lineis curvis quarum revolutione curvæ illæ superficies genitæ sunt. Istis igitur in casibus sufficit motum in his lineis curvis considerare.
Prop. XLVIII. Theor. XVI.
Si rota globo extrinsecus ad angulos rectos insistat, & more rotarum revolvendo progrediatur in circulo maximo; longitudo itineris curvilinei, quod punctum quodvis in rotæ perimetro datum, ex quo globum tetigit, confecit, erit ad duplicatum sinum versum arcus dimidii qui globum ex eo tempore inter eundem tetigit, ut summa diametrorum globi & rotæ ad semidiametrum globi.
Prop. XLIX. Theor. XVII.
Si rota globo concavo ad rectos angulos intrinsecus insistat & revolvendo progrediatur in circulo maximo; longitudo itineris curvilinei quod punctum quodvis in Rotæ Perimetro datum, ex quo globum tetigit, confecit, erit ad duplicatum sinum versum arcus dimidii qui globum toto hoc tempore inter eundum tetigit, ut differentia diametrorum globi & rotæ ad semidiametrum globi.
Sit ABL globus, C centrum ejus, BPV rota ei insistens, E centrum rotæ, B punctum contactus, & P punctum datum in perimetro rotæ. Concipe hanc Rotam pergere in circulo maximo ABL ab A per B versus L, & inter eundum ita revolvi ut arcus AB, PB sibi invicem semper æquentur, atq; punctum illud P in Perimetro rotæ datum interea describere viam curvilineam AP. Sit autem AP via tota curvilinea descripta ex quo Rota globum tetigit in A, & erit viæ hujus longitudo AP ad duplum sinum versum arcus ½PB, ut 2CE ad CB. Nam recta CE (si opus est producta) occurrat Rotæ in V, junganturq; CP, BP, EP, VP, & in CP productam demittatur Normalis VF. Tangant PH, VH circulum in P & V concurrentes in H, secetq; PH ipsam VF in G, & ad VP demittantur Normales GI, HK. Centro item C & intervallo quovis describatur circulus nom secans rectam CP in n, Rotæ perimetrum Bp in o & viam curvilineam AP in m, centroq; V & intervallo Vo describatur circulus secans VP productam in q.
Quoniam Rota eundo semper revolvitur circa punctum contactus B, manifestum est quod recta BP perpendicularis est ad lineam illam curvam AP, quam Rotæ punctum P describit, atq; adeo quod recta VP tanget hanc curvam in puncto P. Circuli nom radius sensim auctus æquetur tandem distantiæ CP, & ob similitudinem figuræ evanescentis Pnomq & figuræ PFGVI, ratio ultima lineolarum evanescentium Pm, Pn, Po, Pq, id est ratio incrementorum momentaneorum curvæ AP, rectæ CP & arcus circularis BP, ac decrementi rectæ VP, eadem erit quæ linearum PV, PF, PG, PI respective. Cum autem VF ad CF & VH ad CV perpendiculares sunt, anguliq; HVG, VCF propterea æquales; & angulus VHP, (ob angulos quadrilateri HVEP ad V & P rectos,) complet angulum VEP ad duos rectos, adeoq; angulo CEP æqualis est, similia erunt triangula VHG, CEP; & inde fiet ut EP ad CE ita HG ad HV seu HP, & ita KI ad KP, & divisim ut CB ad CE ita PI ad PK, & duplicatis consequentibus ut CB ad 2CE ita PI ad PV. Est igitur decrementum lineæ VP, id est incrementum lineæ BV - VP, ad incrementum lineæ curvæ AP in data ratione CB ad 2CE, & propterea (per Corol. Lem. IV.) longitudines BV - VP & AP incrementis illis genitæ sunt in eadem ratione. Sed existente BV radio, est VP cosinus anguli VPB seu ½BEP, adeoq; BV - VP sinus versus ejusdem anguli, & propterea in hac Rota cujus radius est ½BV, erit BV - VP duplus sinus versus arcus ½BP. Ergo AP est ad duplum sinum versum arcus ½BP ut 2CE ad CB. Q. E. D.
Lineam autem AP in Propositione priore Cycloidem extra Globum, alteram in posteriore Cycloidem intra Globum distinctionis gratia nominabimus.
Corol. 1. Hinc si describatur Cyclois integra ASL & bisecetur ea in S, erit longitudo partis PS ad longitudinem VP (quæ duplus est sinus anguli VBP, existente EB radio) ut 2CE ad CB atq; adeo in ratione data.
Corol. 2. Et longitudo semiperimetri Cycloidis AS æquabitur lineæ rectæ, quæ est ad Rotæ diametrum BV ut 2CE ad CB.
Corol. 3. Ideoq; longitudo illa est ut rectangulum BEC, si modo Globi detur semidiameter.
Prop. L. Prob. XXXIII.
Facere ut Corpus pendulum oscilletur in Cycloide data.
Intra Globum QVS centro C descriptum detur Cyclois QRS bisecta in R & punctis suis extremis Q & S superficiei Globi hinc inde occurrens. Agatur CR bisecans arcum QS in O, & producatur ea ad A, ut sit CA ad CO ut CO ad CR. Centro C intervallo CA describatur Globus exterior ABD, & intra hunc globum Rota, cujus diameter sit AO, describantur duæ semicycloides AQ, AS, quæ globum interiorem tangant in Q & S & globo exteriori occurrant in A. A puncto illo A, filo APT longitudinem AR æquante, pendeat corpus T, & ita intra semicycloides AQ, AS oscilletur, ut quoties pendulum digreditur a perpendiculo AR, filum parte sui superiore AP applicetur ad semicycloidem illam APS, versus quam peragitur motus, & circum eam ceu obstaculum flectatur, parteq; reliqua PT cui semicyclois nondum objicitur, protendatur in lineam rectam; & pondus T oscillabitur in Cycloide data QRS. Q. E. F.
Occurrat enim filum PT tum Cycloidi QRS in T, tum circulo QOS in V, agaturq; CV occurrens circulo ABD in B; & ad fili partem rectam PT, e punctis extremis P ac T, erigantur perpendicula PB, TW, occurrentia rectæ CV in B & W. Patet enim ex genesi Cycloidis, quod perpendicula illa PB, TW, abscindent de CV longitudines VB, VW rotarum diametris OA, OR æquales, atq; adeo quod punctum B incidet in circulum ABD. Est igitur TP ad VP (duplum sinum anguli VBP existente ½BV radio) ut BW ad BV, seu AO + OR ad AO, id est (cum sint CA ad CO, CO ad CR & divisim AO ad OR proportionales,) ut CA + CO seu 2CE ad CA. Proinde per Corol. 1. Prop. XLIX. longitudo PT æquatur Cycloidis arcui PS, & filum totum APT æquatur Cycloidis arcui dimidio APS, hoc est (per Corollar. 2. Prop. XLIX) longitudini AR. Et propterea vicissim si filum manet semper æquale longitudini AR movebitur punctum T in Cycloide QRS. Q. E. D.
Corol. Filum AR æquatur Cycloidis arcui dimidio APS.
Prop. LI. Theor. XVIII.
Nam in Cycloidis tangentem TW infinite productam cadat perpendiculum CX & jungatur CT. Quoniam vis centripeta qua corpus T impellitur versus C est ut distantia CT, (per Legum Corol. 2.) resolvitur in partes CX, TX, quarum CX impellendo corpus directe a P distendit filum PT & per cujus resistentiam tota cessat, nullum alium edens effectum; pars autem altera TX urgendo corpus transversim seu versus X, directe accelerat motum ejus in Cycloide; manifestum est quod corporis acceleratio huic vi acceleratrici proportionalis sit singulis momentis ut longitudo TX, id est, ob datas CV, WV iisq; proportionales TX, TW, ut longitudo TW, hoc est (per Corol. 1. Prop. XLIX.) ut longitudo arcus Cycloidis TR. Pendulis igitur duabus APT, Apt de perpendiculo AR inæqualiter deductis & simul dimissis, accelerationes eorum semper erunt ut arcus describendi TR, tR. Sunt autem partes sub initio descriptæ ut accelerationes, hoc est ut totæ sub initio describendæ, & propterea partes quæ manent describendæ & accelerationes subsequentes his partibus proportionales sunt etiam ut totæ; & sic deinceps. Sunt igitur accelerationes atq; adeo velocitates genitæ & partes his velocitatibus descriptæ partesq; describendæ, semper ut totæ; & propterea partes describendæ datam servantes rationem ad invicem simul evanescent, id est corpora duo oscillantia simul pervenient ad perpendiculum AR. Cumq; vicissim ascensus perpendiculorum de loco infimo R, per eosdem arcus Trochoidales motu retrogrado facti, retardentur in locis singulis a viribus iisdem a quibus descensus accelerabantur, patet velocitates ascensuum ac descensuum per eosdem arcus factorum æquales esse, atq; adeo temporibus æqualibus fieri; & propterea, cum Cycloidis partes duæ RS & RQ ad utrumq; perpendiculi latus jacentes sint similes & æquales, pendula duo oscillationes suas tam totas quam dimidias iisdem temporibus semper peragent. Q. E. D.
Prop. LII. Prob. XXXIV.
Definire & velocitates Pendulorum in locis singulis, & Tempora quibus tum oscillationes totæ, tum singulæ oscillationum partes peraguntur.
Centro quovis G, intervallo GH Cycloidis arcum RS æquante, describe semicirculum HKMG semidiametro GK bisectum. Et si vis centripeta distantiis locorum a centro proportionalis tendat ad centrum G, sitq; ea in perimetro HIK æqualis vi centripetæ in perimetro globi QOS (Vide Fig. Prop. L. & LI.) ad ipsius centrum tendente; & eodem tempore quo pendulum T dimittitur e loco supremo S, cadat corpus aliquod L ab H ad G: quoniam vires quibus corpora urgentur sunt æquales sub initio & spatiis describendis TR, GL semper proportionales, atq; adeo, si æquantur TR & LG, æquales in locis T & L; patet corpora illa describere spatia ST, HL æqualia sub initio, adeoq; subinde pergere æqualiter urgeri, & æqualia spatia describere. Quare, per Prop. XXXVIII., tempus quo corpus describit arcum ST est ad tempus oscillationis unius, ut arcus HI (tempus quo corpus H perveniet ad L) ad semicirculum HKM (tempus quo corpus H perveniet ad M.) Et velocitas corporis penduli in loco T est ad velocitatem ipsius in loco infimo R, (hoc est velocitas corporis H in loco L ad velocitatem ejus in loco G, seu incrementum momentaneum lineæ HL ad incrementum momentaneum lineæ HG, arcubus HI, HK æquabili fluxu crescentibus) ut ordinatim applicata LI ad radium GK, sive ut √SRq. - TRq. ad SR. Unde cum in Oscillationibus inæqualibus describantur æqualibus temporibus arcus totis Oscillationum arcubus proportionales, habentur ex datis temporibus & velocitates & arcus descripti in Oscillationibus universis. Quæ erant primo invenienda.
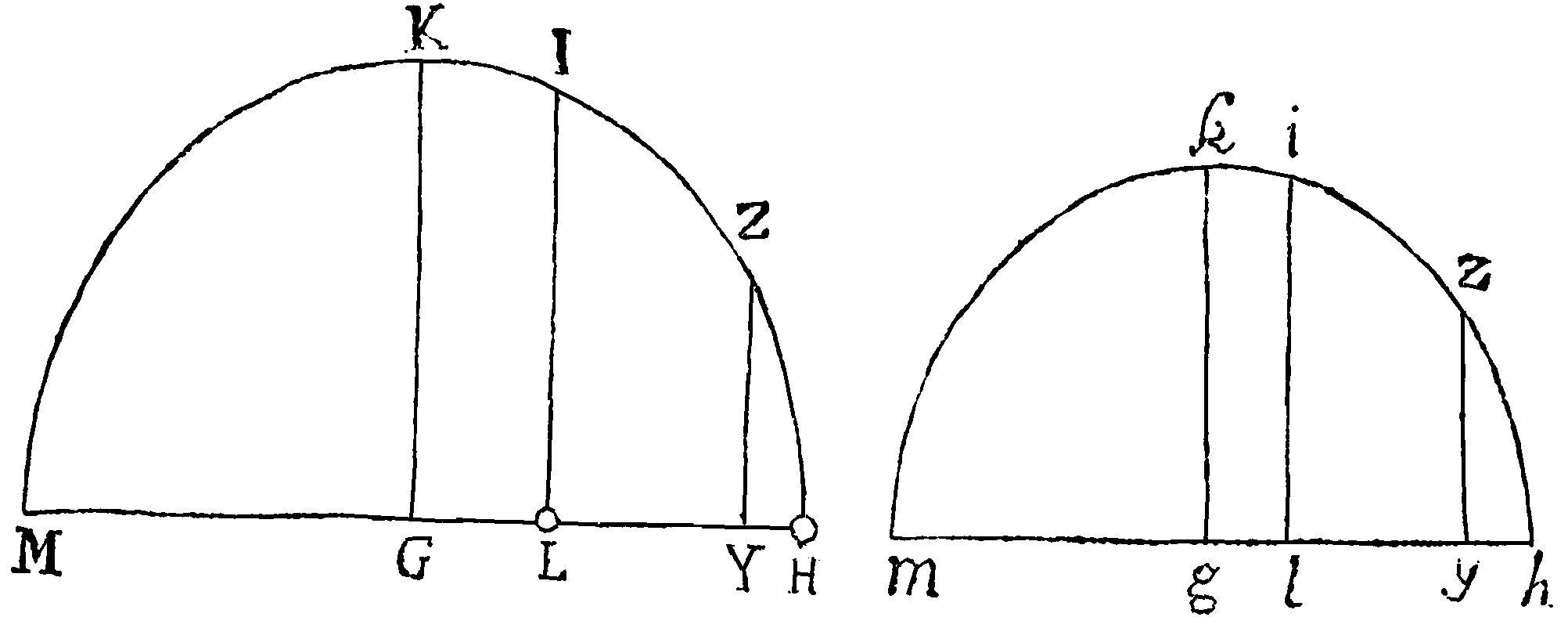
Oscillentur jam funipendula duo corpora in Cycloidibus inæqualibus & earum semiarcubus æquales capiantur rectæ GH, gh, centrisq; G, g & intervallis GH, gh describantur semicirculi HZKM, hzkm. In eorum diametris HM, hm capiantur lineolæ æquales HY, hy, & erigantur normaliter YZ, yz circumferentiis occurrentes in Z & z. Quoniam corpora pendula sub initio motus versantur in circumferentia globi QOS, adeoq; a viribus æqualibus urgentur in centrum, incipiuntq; directe versus centrum moveri, spatia simul consecta æqualia erunt sub initio. Urgeantur igitur corpora H, h a viribus iisdem in H & h, sintq; HY, hy spatia æqualia ipso motus initio descripta, & arcus HZ, hz denotabunt æqualia tempora. Horum arcuum nascentium ratio prima duplicata est eadem quæ rectangulorum GHY, ghy, id est, eadem quæ linearum GH, gh adeoq; arcus capti in dimidiata ratione semidiametrorum denotant æqualia tempora. Est ergo tempus totum in circulo HKM, Oscillationi in una Cycloide respondens, ad tempus totum in circulo hkm Oscillationi in altera Cycloide respondens, ut semiperiferia HKM ad medium proportionale inter hanc semiperiferiam & semiperiferiam circuli alterius hkm, id est in dimidiata ratione diametri HM ad diametrum hm, hoc est in dimidiata ratione perimetri Cycloidis primæ ad perimetrum Cycloidis alterius, adeoq; tempus illud in Cycloide quavis est (per Corol. 3. Prop. XLIX.) ut latus quadratum rectanguli BEC contenti sub semidiametro Rotæ, qua Cyclois descripta fuit, & differentia inter semidiametrum illam & semidiametrum globi. Q. E. I. Est & idem tempus (per Corol. Prop. L.) in dimidiata ratione longitudinis fili AR. Q. E. I.
Porro si in globis concentricis describantur similes Cycloides: quoniam earum perimetri sunt ut semidiametri globorum & vires in analogis perimetrorum locis sunt ut distantiæ locorum a communi globorum centro, hoc est ut globorum semidiametri, atq; adeo ut Cycloidum perimetri & perimetrorum partes similes, æqualia erunt tempora quibus perimetrorum partes similes Oscillationibus similibus describuntur, & propterea Oscillationes omnes erunt Isochronæ. Cum igitur Oscillationum tempora in Globo dato sint in dimidiata ratione longitudinis AR, atq; adeo (ob datam AC) in dimidiata ratione numeri AR ÷ AC, id est in ratione integra numeri √{AR ÷ AC}; & hic numerus √{AR ÷ AC} servata ratione AR ad AC (ut fit in Cycloidibus similibus) idem semper maneat, & propterea in globis diversis, ubi Cycloides sunt similes, sit ut tempus: manifestum est quod Oscillationum tempora in alio quovis globo dato, atq; adeo in globis omnibus concentricis sunt ut numerus √{AR ÷ AC}, id est, in ratione composita ex dimidiata ratione longitudinis fili AR directe & dimidiata ratione semidiametri globi AC inverse. Q. E. I.
Deniq; si vires absolutæ diversorum globorum ponantur inæquales, accelerationes temporibus æqualibus factæ, erunt ut vires. Unde si tempora capiantur in dimidiata ratione virium inverse, velocitates erunt in eadem dimidiata ratione directe, & propterea spatia erunt æqualia quæ his temporibus describuntur. Ergo Oscillationes in globis & Cycloidibus omnibus, quibuscunq; cum viribus absolutis factæ, sunt in ratione quæ componitur ex dimidiata ratione longitudinis Penduli directe, & dimidiata ratione distantiæ inter centrum Penduli & centrum globi inverse, & dimidiata ratione vis absolutæ etiam inverse, id est, si vis illa dicatur V, in ratione numeri √{AR ÷ {AC × V}}. Q. E. I.
Corol. 1. Hinc etiam Oscillantium, cadentium & revolventium corporum tempora possunt inter se conferri. Nam si Rotæ, qua Cyclois intra globum describitur, diameter constituatur æqualis semidiametro globi, Cyclois evadet linea recta per centrum globi transiens, & Oscillatio jam erit descensus & subsequens ascensus in hac recta. Unde datur tum tempus descensus de loco quovis ad centrum, tum tempus huic æquale quo corpus uniformiter circa centrum globi ad distantiam quamvis revolvendo arcum quadrantalem describit. Est enim hoc tempus (per Casum secundum) ad tempus semioscillationis in Trochoide quavis APS ut ½BC ad √BEC.
Corol. 2. Hinc etiam consectantur quæ D. C. Wrennus & D. C. Hugenius de Cycloide vulgari adinvenerunt. Nam si globi diameter augeatur in infinitum, mutabitur ejus superficies Sphærica in planum, visq; centripeta aget uniformiter secundum lineas huic plano perpendiculares, & Cyclois nostra abibit in Cycloidem vulgi. Isto autem in casu, longitudo arcus Cycloidis, inter planum illud & punctum describens, æqualis evadet quadruplicato sinui verso dimidii arcus Rotæ inter idem planum & punctum describens; ut invenit D. C. Wrennus: Et pendulum inter duas ejusmodi Cycloides in simili & æquali Cycloide temporibus æqualibus Oscillabitur, ut demonstravit Hugenius. Sed & descensus gravium, tempore Oscillationis unius, is erit quem Hugenius indicavit.
Aptantur autem Propositiones a nobis demonstratæ ad veram constitutionem Terræ, quatenus Rotæ eundo in ejus circulis maximis describunt motu clavorum Cycloides extra globum; & Pendula inferius in fodinis & cavernis Terra suspensa, in Cycloidibus intra globos Oscillari debent, ut Oscillationes omnes evadant Isochronæ. Nam Gravitas (ut in Libro tertio docebitur) decrescit in progressu a superficie Terræ, sursum quidem in duplicata ratione distantiarum a centro ejus, deorsum vero in ratione simplici.
Prop. LIII. Prob. XXXV.
Concessis figurarum curvilinearum Quadraturis, invenire vires quibus corpora in datis curvis lineis Oscillationes semper Isochronas peragent.
Oscilletur corpus T in curva quavis linea STRQ, cujus axis sit OR transiens per virium centrum C. Agatur TX quæ curvam illam in corporis loco quovis T contingat, inq; hac Tangente TX capiatur TY æqualis arcui TR. Nam longitudo arcus illius ex figurarum Quadraturis per Methodos vulgares innotescit. De puncto Y educatur recta YZ Tangenti perpendicularis. Agatur CT perpendiculari illi occurrens in Z, & erit vis centripeta proportionalis rectæ TZ. Q. E. I.
Nam si vis, qua corpus trahitur de T versus C, exponatur per rectam TZ captam ipsi proportionalem, resolvetur hæc in vires TY, YZ; quarum YZ trahendo corpus secundum longitudinem fili PT, motum ejus nil mutat, vis autem altera TY motum ejus in curva STRQ directe accelerat vel directe retardat. Proinde cum hæc sit ut via describenda TR, accelerationes corporis vel retardationes in Oscillationum duarum (majoris & minoris) partibus proportionalibus describendis, erunt semper ut partes illæ, & propterea facient ut partes illæ simul describantur. Corpora autem quæ partes totis semper proportionales simul describunt, simul describent totas. Q. E. D.
Corol. 1. Hinc si corpus T filo rectilineo AT a centro A pendens, describat arcum circularem STRQ, & interea urgeatur secundum lineas parallelas deorsum a vi aliqua, quæ sit ad vim uniformem gravitatis, ut arcus TR ad ejus sinum TN: æqualia erunt Oscillationum singularum tempora. Etenim ob parallelas TZ, AR, similia erunt triangula ANT, TYZ; & propterea TZ erit ad AT ut TY ad TN; hoc est, si gravitatis vis uniformis exponatur per longitudinem datam AT, vis TZ, qua Oscillationes evadent Isochronæ, erit ad vim gravitatis AT, ut arcus TR ipsi TY æqualis ad arcus illius sinum TN.
Corol. 2. Igitur in Horologiis, si vires a Machina in Pendulum ad motum conservandum impressæ ita cum vi gravitatis componi possint, ut vis tota deorsum semper sit ut linea quæ oritur applicando rectangulum sub arcu TR & radio AR, ad sinum TN, Oscillationes omnes erunt Isochronæ.
Prop. LIV. Prob. XXXVI.
Concessis figurarum curvilinearum quadraturis, invenire tempora quibus corpora vi qualibet centripeta in lineis quibuscunq; curvis in plano per centrum virium transeunte descriptis, descendent & ascendent.