Diffraction By Multiple Slits: Diffraction Grating
Diffraction by multiple slits: Diffraction Grating: In earlier lecture, we have seen the effect on intensity distribution when the light waves passe through two nearby narrow slits. As a result of this, the broad principal maximum produced by single slit actually consists of alternate dark and bright region. Now we will see the combined effect of interference and diffraction on intensity distribution, when the light waves are allowed to pass through large number of narrow slits, very close to each other. This arrangement of slits(Fig.12.3.1 ) is known as diffraction grating and finds lots of application in optics. Once again, each of these slits acts as source of secondary wavelengths and we will see again combined effect of interference and diffraction on screen. In this case, the broad principal maxima corresponding to single slit pattern, consists of several principal maxima and very low intensity secondary maxima separated by minima. We assume that width of each slit is ‘d' and the separation between the centers of any two adjacent slits is ‘b'. We will calculate the resultant intensity at the point P on the screen due to N such slits.
In order to find intensity distribution, we have to calculate the resultant amplitude of all waves reaching the point P . These wavelets are now originating from N slits and the calculation of the amplitude, as we did in case of single slit and double slit, is complicated. However, we can use the complex amplitude method. Here we note that the phase difference between the waves originating from similar position of two consecutive slits is 
( b is separation between the two slits). The amplitude part from each wave is 
Thus if we have two slits
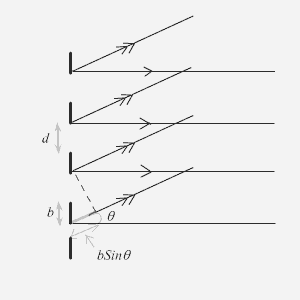Fig.A
Where , 
, 
and resultant intensity 
(where 
) This expression is same as the one obtained for two slits in the previous section.
Now in case on N slits, the resultant amplitude can be written as
which is a geometrical series
the resultant intensity at P due to N slits is
