Optics: Diffraction

Optics: Diffraction: If an opaque obstacle (or aperture) is placed between a source of light and screen, a sufficiently distinct shadow of opaque (or an illuminated aperture) is obtained on the screen .This shows that the light travels approximately in a straight lines. If, however, the size of obstacle (or aperture) is small (comparable with the wavelength of light), there is a departure from straight line propagation and the light bends round the corners of the obstacles(or aperture) and enters the geometrical shadow. The bending of light at sharp corners/edges is called diffraction. As a result of diffraction, the edges of the shadow (or illuminated region) are not sharp , but the intensity is distributed in a certain way depending upon the nature of obstacle (or aperture).

Let us first explain, how the light bends around a sharp corner. According to Huygen's principle, when a wave propagates, each point on its wave front serves as the source of spherical secondary wavelets having same frequency as that of original wave [Fig. 1a]. The resultant at any point afterward is the envelope of these secondary wavelets. However, this picture does not explain the diffraction of light through small apertures.

If we assume that, as shown in fig.1b, each unobstructed point of a wavefront, at a given instant, serves as a source of spherical secondary wavefront, the amplitude of the optical field at any point beyond is the superposition of all these wavefronts. The maximum path difference between these secondary wave fronts at any point P is equal to AB . (Path difference will be equal to AB if point P merges with either point A or point B) .

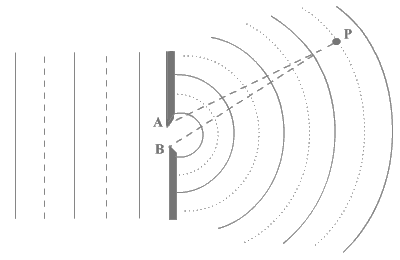Fig : 1a.

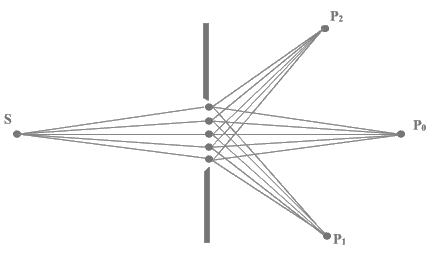Fig: 1b.

Now if , at all the points on far away screen, the waves originating from different parts of the slit will be partially in phase, and we observe finite intensity of wave there. This automatically explains the bending of waves at sharp obstacles.

For , the secondary wavelets originating from the slit, when reach the screen, will have different phases. At points, where path difference is zero (point on the screen for which the line joining center of slit to screen is perpendicular to the plane of slit), the intensity will be maximum and will slowly diminish as we move further away from this point. At point where path difference become the minima will be observed and as we move further again the intensity will increase.