Principles Of X-ray Diffraction
Principles of X-ray Diffraction: Diffraction effects are observed when electromagnetic radiation impinges on periodic structures with geometrical variations on the length scale of the wavelength of the radiation. The interatomic distances in crystals and molecules amount to 0.15–0.4 nm which correspond in the electromagnetic spectrum with the wavelength of x-rays having photon energies between 3 and 8 keV. Accordingly, phenomena like constructive and destructive interference should become observable when crystalline and molecular structures are exposed to x-rays. In the following sections, firstly, the geometrical constraints that have to be obeyed for x-ray interference to be observed are introduced. Secondly, the results are exemplified by introducing the θ/2θ scan, which is a major x-ray scattering technique in thin-film analysis. Thirdly, the θ/2θ diffraction pattern is used to outline the factors that determine the intensity of x-ray ref lections. We will thereby rely on numerous analogies to classical optics and frequently use will be made of the fact that the scattering of radiation has to proceed coherently, i.e. the phase information has to be sustained for an interference to be observed. In addition, the three coordinate systems as related to the crystal {ci}, to the sample or specimen {s} and to the laboratory {li} that have to be considered in diffraction are introduced. Two instrumental sections (Instrumental Boxes 1 and 2) related to the θ/2θ diffractometer and the generation of x-rays by x-ray tubes supplement the chapter. One-elemental metals and thin films composed of them will serve as the material systems for which the derived principles are demonstrated. A brief presentation of one-elemental structures is given in Structure Box1.
The Basic Phenomenon:Before the geometrical constraints for x-ray interference are derived the interactions between x-rays and matter have to be considered. There are three different types of interaction in the relevant energy range. In the first, electrons may be liberated from their bound atomic states in the process of photoionization. Since energy and momentum are transferred from the incoming radiation to the excited electron, photoionization falls into the group of inelastic scattering processes. In addition, there exists a second kind of inelastic scattering that the incoming x-ray beams may undergo, which is termed Compton scattering. Also in this process energy is transferred to an electron, which proceeds, however, without releasing the electron from the atom. Finally, x-rays may be scattered elastically by electrons, which is named Thomson scattering. In this latter process the electron oscillates like a Hertz dipole at the frequency of the incoming beam and becomes a source of dipole radiation. The wavelength λ of x-rays is conserved for Thomson scattering in contrast to the two inelastic scattering processes mentioned above. It is the Thomson component in the scattering of x-rays that is made use of in structural investigations by x-ray diffraction.
Figure 1 illustrates the process of elastic scattering for a single free electron of charge e, mass mand at position R0. The incoming beam is accounted for by a plane wave E0exp(–iK0R0), where E0 is the electrical field vector and K0 the wave vector.
The dependence of the field on time will be neglected throughout. The wave vectors K0 and K describe the direction of the incoming and exiting beam and both are
of magnitude 2π/λ. They play an important role in the geometry of the scattering process and the plane defined by them is denoted as the scattering plane. The angle between K and the prolonged direction of K0 is the scattering angle that will be abbreviated by 2θ as is general use in x-ray diffraction. We may also define it by the two wave vectors according to
............................eq..(1)
The formula is explicitly given here, because the definition of angles by two adjoining vectors will be made use of frequently. The oscillating charge e will emit radiation of the same wavelength λ as the primary beam. In fact, a phase shift of 180° occurs with the scattering, but since this shift equally arises for every scattered wave it has no effect on the interference pattern in which we are interested and will be neglected. If the amplitude of the scattered wave E(R) is considered at a distance R we may write according to Hertz and Thomson
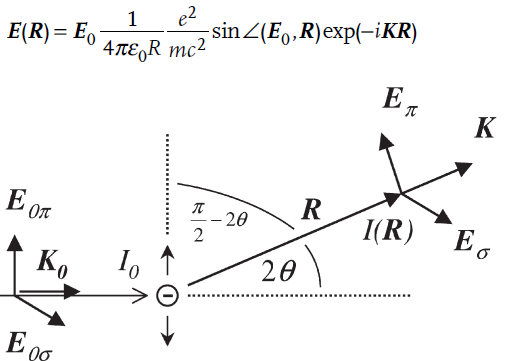Figure A Scattering of x-rays by a single electron.