Measure Of Central Tendency

Measures of Central Tendency:

1.       Measures of central tendency are measures of the location of the middle or the center of a distribution.

2.       The mean is the most commonly used measure of central tendency.

3.       Thearithmetic mean is what is commonly called the average, the sum of all the observations divided by the number of observations in a sample or in a population.

4.       The mean of a population is expressed mathematically as

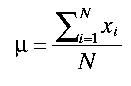
Where N is the number of population observations. The average of a sample j is expressed mathematically as

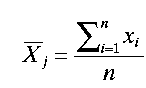
Where n is the sample size.

 

5.       Themean is a good measure of central tendency for roughly symmetric distributions but can be misleading in skewed distributions since it can be greatly influenced by extreme observations. Therefore, other statistics, such as the median and mode, may be more informative for skewed distributions.

6.       The mean, median, and mode are equal in symmetric distributions.

7.       Themean is higher than the median in positively skewed distributions and lower than the median in negatively skewed distributions.

8.       The median is the middle of a distribution, where half the scores are above the median and half are below the median. The median is less sensitive than the mean to extreme scores, and this makes it a better measure than the mean for highly skewed distributions.

9.       The modeis the most frequently occurring score in a distribution. The advantage of the mode as a measure of central tendency is that it has an obvious meaning. Further, it is the only measure of central tendency that can be used with nominal data (it is not computed).

10.   The mode is sensitive to sample fluctuation and is therefore not recommended to be used as the only measure of central tendency. A further disadvantage of the mode is that many distributions have more than one mode. These distributions are called multimodal.