Cancellation Of Poles G(s) With Zeros Of H(s)

Cancellation of poles G(s) with zeros of H(s):

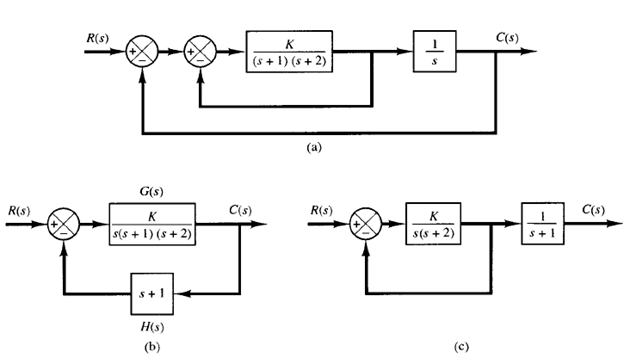
Fig: 1

 If the denominator of G(s) and the numerator of H(s) involve common factors then the corresponding open-loop poles and zeros will cancel each other, reducing the degree of the characteristic equation by one or more.

 For example, consider the system shown in Figure 1(a). (This system has velocity feedback.)

 By modifying the block diagram of Figure 1(a) to that shown in Figure 1(b), it is clearly seen that G(s) and H(s) have a common factor s 1.

 The closed-loop transfer function C(s)/R(s) is

The root-locus plot of G(s)H(s) does not show all the roots of the characteristic equation, only the roots of the reduced equation.

To obtain the complete set of closed-loop poles, we must add the canceled pole of G(s)H(s) to those closed-loop poles obtained from the root-locus plot of G(s)H(s). The important thing to remember is that the canceled pole of G(s)H(s) is a closed-loop pole of the system, as seen from Figure 1(c).