←
Control Systems - 1
Jury's Stability Test
Jury's stability test
For the Jury Test for stability of a discrete-time system, let us consider a transfer function
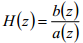
the system is stable if and only if all roots of 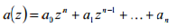 are inside the unit circle.
are inside the unit circle.
To use the Jury test, begin by multiplying a(z) by -1 if necessary to make a0 positive. Then form the following array:
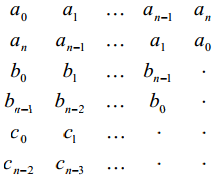
Third-row entries are based on second-order determinants divided by a0 of the first two rows, starting with the first and last columns, then the first and second-to-last columns, etc.:
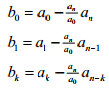
The fourth row is made by reversing the third row, and the fifth row is given by
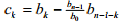
If all the terms in the first columns of the odd rows are positive, the polynomial a(z) is stable.