Flow Networks
An example of flow: A flow network can model the trucking problem shown in Figure 26.1(a). The Lucky Puck Company has a factory (source s) in Vancouver that manufactures hockey pucks, and it has a warehouse (sink t) in Winnipeg that stocks them. Lucky Puck leases space on trucks from another firm to ship the pucks from the factory to the warehouse. Because the trucks travel over specified routes (edges) between cities (vertices) and have a limited capacity, Lucky Puck can ship at most c(u, v) crates per day between each pair of cities u and v in Figure 26.1(a). Lucky Puck has no control over these routes and capacities and so cannot alter the flow network shown in Figure 26.1(a). Their goal is to determine the largest number p of crates per day that can be shipped and then to produce this amount, since there is no point in producing more pucks than they can ship to their warehouse. Lucky Puck is not concerned with how long it takes for a given puck to get from the factory to the warehouse; they care only that p crates per day leave the factory and p crates per day arrive at the warehouse.
- On the surface, it seems appropriate to model the "flow" of shipments with a flow in this network because the number of crates shipped per day from one city to another is subject to a capacity constraint. Additionally, flow conservation must be obeyed, for in a steady state, the rate at which pucks enter an intermediate city must equal the rate at which they leave. Otherwise, crates would accumulate at intermediate cities.
- There is one subtle difference between shipments and flows, however. Lucky Puck may ship pucks from Edmonton to Calgary, and they may also ship pucks from Calgary to Edmonton. Suppose that they ship 8 crates per day from Edmonton (v1 in Figure 26.1) to Calgary (v2) and 3 crates per day from Calgary to Edmonton. It may seem natural to represent these shipments directly by flows, but we cannot. The skew-symmetry constraint requires that f (v1, v2) = - f (v2, v1), but this is clearly not the case if we consider f(v1, v2) = 8 and f(v2, v1) = 3.
- Lucky Puck may realize that it is pointless to ship 8 crates per day from Edmonton to Calgary and 3 crates from Calgary to Edmonton, when they could achieve the same net effect by shipping 5 crates from Edmonton to Calgary and 0 crates from Calgary to Edmonton (and presumably use fewer resources in the process). We represent this latter scenario with a flow: we have f (v1, v2) = 5 and f(v2, v1) = -5. In effect, 3 of the 8 crates per day from v1 to v2 are canceled by 3 crates per day from v2 to v1.
- In general, cancellation allows us to represent the shipments between two cities by a flow that is positive along at most one of the two edges between the corresponding vertices. That is, any situation in which pucks are shipped in both directions between two cities can be transformed using cancellation into an equivalent situation in which pucks are shipped in one direction only: the direction of positive flow.
- Given a flow f that arose from, say, physical shipments, we cannot reconstruct the exact shipments. If we know that f(u, v) = 5, this flow may be because 5 units were shipped from u to v, or it may be because 8 units were shipped from u to v and 3 units were shipped from v to u. Typically, we shall not care how the actual physical shipments are set up; for any pair of vertices, we care only about the net amount that travels between them. If we do care about the underlying shipments, then we should be using a different model, one that retains information about shipments in both directions.
- Cancellation will arise implicitly in the algorithms in this chapter. Suppose that edge (u, v) has a flow value of f(u, v). In the course of an algorithm, we may increase the flow on edge (v, u) by some amount d. Mathematically, this operation must decrease f(u, v) by d and, conceptually, we can think of these d units as canceling d units of flow that are already on edge (u, v).
Networks with multiple sources and sinks
A maximum-flow problem may have several sources and sinks, rather than just one of each. The Lucky Puck Company, for example, might actually have a set of m factories {s1, s2, . . . , sm} and a set of n warehouses {t1, t2, . . . , tn}, as shown in Figure 26.2(a). Fortunately, this problem is no harder than ordinary maximum flow.
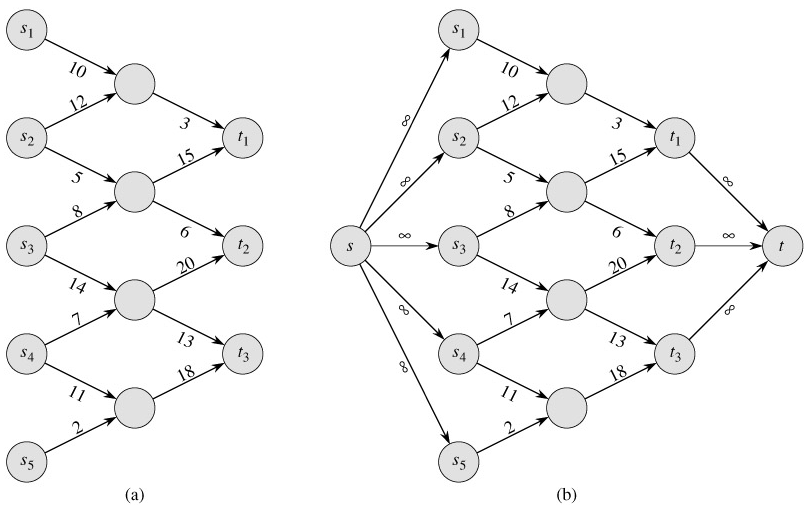
We can reduce the problem of determining a maximum flow in a network with multiple sources and multiple sinks to an ordinary maximum-flow problem. Figure 26.2(b) shows how the network from (a) can be converted to an ordinary flow network with only a single source and a single sink. We add a supersource s and add a directed edge (s, si) with capacity c(s, si) = ∞ for each i = 1, 2, . . . , m. We also create a new supersink t and add a directed edge (ti, t) with capacity c(ti, t) = ∞ for each i = 1, 2, . . . , n. Intuitively, any flow in the network in (a) corresponds to a flow in the network in (b), and vice versa. The single source s simply provides as much flow as desired for the multiple sources si, and the single sink t likewise consumes as much flow as desired for the multiple sinks ti.
Working with flows
We shall be dealing with several functions (like f) that take as arguments two vertices in a flow network. In this chapter, we shall use an implicit summation notation in which either argument, or both, may be a set of vertices, with the interpretation that the value denoted is the sum of all possible ways of replacing the arguments with their members. For example, if X and Y are sets of vertices, then
Thus, the flow-conservation constraint can be expressed as the condition that f(u, V) = 0 for all u ∈ V - {s, t}. Also, for convenience, we shall typically omit set braces when they would otherwise be used in the implicit summation notation. For example, in the equation f (s, V - s) = f(s, V), the term V - s means the set V - {s}.