Convergence Of Fourier Series

Convergence of Fourier Series:

For each positive integer N, let

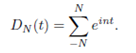
This function is continuous and periodic with periods 2π. Note also that

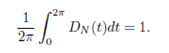
The function D_N is called the Dirichlet Kernel.

Preposition 2 If t is not an integer multiple of 2π, then

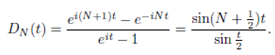
Proof : To obtain the first equality, note that e^it = 1 if and only if t is an integer multiple of 2π. Hence

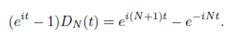
The second follow by multiplying and dividing the second expression by e^it/2, together with 2i sinz = e^iz - e^-iz

Proposition 3 If f is integrable, then

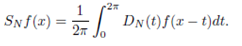
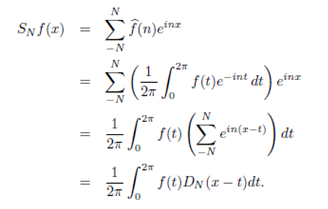
A change of variables x - t = s finishes the proof.

We say that a function f : [0, 2π] → C satiesfies a Lipschitz condition if there is positive constant M such that the periodic extension of f-satiesfies

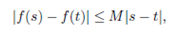
In terms of the functions f defined in [0, 2π] this can be expressed as;

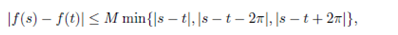
for all s, t ε [0, 2π] . The min is the distance from s to t modulo 2π, and so it is the distance as measured on a circle of length 2π.