Theorem On Inverse Fourier Transform

Theorem on Inverse Fourier Transform:

Theorem. Let f ∈ L¹ (R) and let f be piecewise smooth on R. Then for every x ∈R,

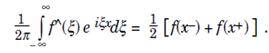
If x is a point of continuity of f, then

For all Φ ∈ L¹ (R), we call The inverse Fourier transform of Φ = f^, then we define;

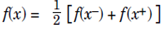at a point of discontinuity of f.

Then 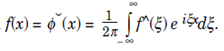That is F^-1Ff = f.

Examples:

The inverse Fourier transform is useful in computing Fourier transforms. Since 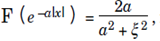It follows that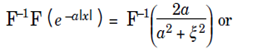

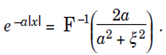
Interchanging the role of x and ξ multiplying by 2π leads to 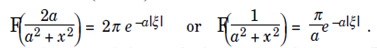In a similar functions every Fourier Series transform pair defines a dual pair using the Inverse Fourier Transform.