Back Propagation Of Error

Introduction:-Thebackpropagation of error learning rule, which can be used to train multistage perceptrons with semi-linear activation. Binary threshold functions and other non-differentiable functions are no longer supported, but that does not matter. The Fermi function or the hyperbolic tangent can arbitrarily approximate the binary threshold function by means of a temperature parameter T.Backpropagation is a gradient descent procedure(including all strengths and weaknesses of the gradient descent) with the error function Err(W) receiving all n weights as arguments and assigning them to the output error, i.e.being n-dimensional. On Err (W) a point of small error or even a point of the smallest error is sought by means of the gradient descent. Thus, in analogy to the delta rule, back propagation trains the weights of the neural network. And it is exactly the delta rule or its variable δi for a neuron i which is expanded from one trainable weight layer to several ones by backpropagation.

1. The derivation is similar to the one of the delta rule, but with a generalized delta

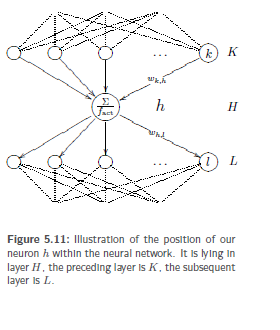
Let us define in advance that the network input of the individual neurons i results from the weighted sum. Furthermore, as with the derivation of the delta rule, let o_p,i, net_p,i etc. be defined as the already familiar o_i, net_i, etc. under the input pattern p we used for the training. Let the output function be the identity again, thus o_i = f_act(net_p,i) holds for any neuron i. Since this is a generalization of the delta rule, we use the same formula frameworkas with the delta rule. It is obvious to select an arbitrary inner neuron h having a set K of predecessor neurons k as well as a set of L successor neurons l, which are also inner neurons. It is therefore irrelevant whether the predecessor neurons are already the input neurons. Now we perform the same derivation as for the delta rule and split functions by means the chain rule.

The error function Err according to a weight w_k,h

------(1)

The first factor of equation -δ_h,.The numerator of the second factor of the equation includes the network input, i.e .the weighted sum is included in the numerator so that can be immediately derived.All summands of the sum drop out apart from the summand containing W_k,h.

This summand is referred to as w_k,h·o_k. If we calculate the derivative, the output of neuron k becomes-

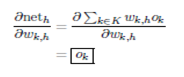-----(2)

We split up equation 1 according of the chain rule:

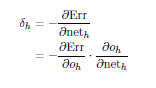----(3)

The derivation of the output according to the network input clearly equals the derivation of the activation function according to the network input:

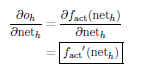----(4)

We now derive the first factor in equation (3). Therefore, we have to point out that the derivation of the error function according to the output of an inner neuron layer depends on the vector of all network inputs of the next following layer. This is reflected in equation (5)

---(5)

According to the definition of the multidimensional chain rule, we immediately obtain equation

--------(6)

The sum in equation (6) contains two factors. These factors being added over the subsequent layer L.We simply calculate the second factor in the following equation

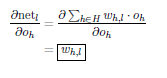---------(7)