Fuzzy Membership

Introduction:-A fuzzy set  A  defined in the universal space  X  is a function defined  in  X  which assumes  values  in  the  range [0, 1]. 

A fuzzy set A   is written as a set of pairs {x, a(x)}.

          A = {{x ,  A(x)}} ,   x in the set X,  where x is an element of the universal space X and  A(x) is the value of the function A for this element.  The value   A(x)   is  the   degree of membership  of  the  element   x in  a  fuzzy  set  A.

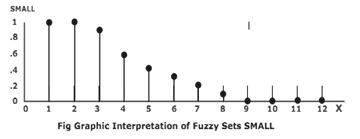
Graphic Interpretation of Fuzzy Sets  SMALL :-The fuzzy set  SMALL  of  small  numbers, defined  in  the  universal spaceX = { xi } = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12}   is presented as   SetOption [FuzzySet,  UniversalSpace → {1, 12, 1}] 

The Set  SMALL in set X  is :  SMALL =  FuzzySet {{1, 1   },   {2, 1  },  {3, 0.9},   {4, 0.6},   {5, 0.4},  {6, 0.3}, {7, 0.2},     {8, 0.1},    {9, 0  },  {10, 0 },   {11, 0},    {12, 0}} Therefore SetSmall is represented as  SetSmall = FuzzySet [{{1,1},{2,1}, {3,0.9}, {4,0.6}, {5,0.4},{6,0.3}, {7,0.2},  {8, 0.1}, {9, 0},  {10, 0}, {11, 0}, {12, 0}} , UniversalSpace → {1, 12, 1}]

FuzzyPlot [ SMALL, AxesLable → {"X", "SMALL"}]

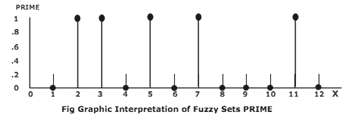
Graphic Interpretation of Fuzzy Sets   PRIME Numbers :-The fuzzy set  PRIME  numbers,  defined  in  the universal space  

X = { xi } = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12}   is presented as   SetOption [FuzzySet,  UniversalSpace → {1, 12, 1}] 

The Set  PRIME  in set X  is : PRIME =  FuzzySet {{1, 0}, {2, 1},  {3, 1},  {4, 0}, {5, 1}, {6, 0},  {7, 1}, {8, 0},    {9, 0}, {10, 0}, {11, 1}, {12, 0}} Therefore SetPrime is represented as  SetPrime = FuzzySet [{{1,0},{2,1}, {3,1}, {4,0}, {5,1},{6,0}, {7,1},  {8, 0}, {9, 0},  {10, 0}, {11, 1}, {12, 0}} , UniversalSpace → {1, 12, 1}]  FuzzyPlot [ PRIME, AxesLable → {"X", "PRIME"}]